2−5.短絡グラフ法
■短絡グラフ法はこれまでに述べてきた因子検定の方法に,より厳密な定式を与えるものであり,ハミルトン検定法の基礎をなすものである.短絡グラフ法では検定の各ステージごとに確定パス上の点を短絡した縮約グラフを作成し,そのグラフ上で新たにハミルトンタイを求めるという方法によって検定を進めてゆく.つまり,短絡グラフ法は完全に再帰的な検定プロセスであり,ハミルトンタイが獲得された時点で停止する.高さN−1の探索木のすべての節点を検査して解が得られなかった場合は,非ハミルトングラフであると結論される.
■短絡グラフ法では検定全域グラフと検定短絡グラフという2種の特殊なグラフを用いて検定を行なう.まず,この2つのグラフに関る定理を証明し,この検定方法が妥当であることを示す.ここではハミルトングラフを,ハミルトンタイをもつ有向グラフであるとする.また,グラフはすべて有向でかつ連結であると仮定する.
定義2-5.1: 検定全域グラフの確定枝集合
グラフGの検定全域グラフの確定枝集合とは,グラフGの入力点ないし出力点を共有しない枝の集合であって,これらの枝のうち隣接する枝を接続してできる枝リストの終点から始点に至る枝を含まないものをいう.
定義2-5.2: 検定全域グラフ
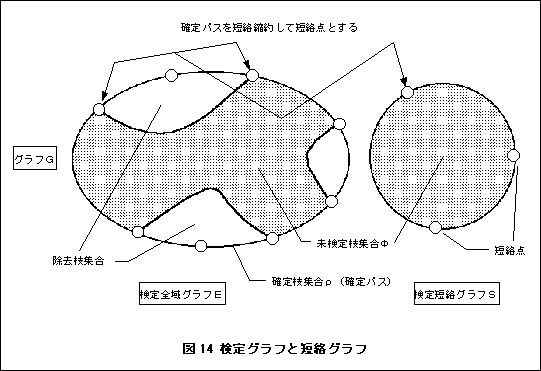
グラフGの検定全域グラフEとはグラフGのすべての点を含む部分グラフであって,確定枝集合ρとρによって規定されるグラフGの未検定枝集合ψの合併を枝集合とするグラフであり,未検定枝集合ψが空でないときにはψに含まれる枝の入力点の入力枝と出力点の出力枝を複数個ψに含むものを言う.ここで未検定枝集合とはグラフGの枝集合の部分枝集合であり,Gの枝集合から確定枝集合ρと,ρのすべての枝の入力点の入力枝,出力点の出力枝および,ρの隣接する枝を接続してできる枝リストの終点から始点に至る枝をすべて除去したものである.定義により検定全域グラフはグラフGの全域部分グラフである.
定義2-5.3: 検定ハミルトングラフ
ハミルトングラフGの検定ハミルトングラフとは,グラフGのハミルトンタイの枝集合の部分集合ρを確定枝集合とするGの検定全域グラフである.検定ハミルトングラフの確定枝集合は定義により矛盾枝を含んでいない.
定義2-5.4: 検定短絡グラフ
グラフGの検定短絡グラフSとは,グラフGの検定全域グラフEの未検定枝集合ψを枝集合とするEの部分グラフにおいて,確定枝集合ρのすべての枝リストの終点と始点を短絡することにより得られるグラフである.Sの枝集合は短絡点のラベルの相違を無視したときψのすべての枝を含んでいる.
定理2-5.1: 検定ハミルトングラフの存在定理
ハミルトングラフGのハミルトンタイに含まれる枝集合の部分集合ρがあるとき,ρを確定枝集合に含むグラフGの検定ハミルトングラフが存在する.
証明:
ρはあるハミルトンタイの部分枝集合であるから,グラフGの入力点ないし出力点を共有する枝は含まれていない.また,これらの枝のうち隣接する枝を接続してできる枝リストの終点から始点に至る枝も含まれていない.
枝集合ρを含む確定枝集合ρ' と,それによって規定されるグラフGの未検定枝集合ψを以下の手順により生成することができる.
(1) 枝集合ρ' =ρとする.グラフGの枝集合から枝集合ρ' を除去した部分枝集合をψとし,ρ' とψの合併を枝集合とするGの部分グラフをG' とする.
(2) ρ' の各枝の入力点の入力枝と出力点の出力枝のすべてをψから除去する.またρ' の枝リストの終点から始点に至る枝があれば同様に除去する.
(3) G’の各点の中で,ψに入力枝ないし,出力枝を1本だけもつ点があればその枝をψからρ' に移動して,(2)を繰り返す.
(4) ψに入力枝ないし,出力枝を1本だけもつ点が無くなれば終わり.
このようにして生成されるグラフG’ には確定枝集合ρ' とそれによって規定される未検定枝集合ψが存在し,未検定枝集合ψが空でないときには,ψに含まれる枝の入力点の入力枝と出力点の出力枝が複数個ψの中に存在しているからG' はグラフGの検定全域グラフである.上記のステップ(2)は因子検定における確定の1ステップに該当するものである.1ステップの動作を定式化して,1ステップ進んだときの枝集合ρ' がつねにハミルトンタイの枝集合の部分枝集合であることを保証できれば,最終的に得られる検定全域グラフは検定ハミルトングラフであることが証明される.以下にこれを示す.
(1) ρはハミルトングラフGのハミルトンタイの部分枝集合であるとする.グラフGの枝集合からρを除去した部分枝集合をψとし,ρとψの合併を枝集合とするGの部分グラフをG' とする.
(2) ρの各枝の入力点の入力枝と出力点の出力枝のすべてをψから除去する.またρの枝リストの終点から始点に至る枝があれば同様に除去する.これらの枝は枝集合ρを含むハミルトンタイに含まれることのない枝である.
(3) Gはハミルトンタイをもち,枝集合ρはハミルトンタイの部分枝集合であるから,枝集合ψには,ρを含むハミルトンタイの枝のうち枝集合ρに含まれない枝のすべてが含まれる.G' の各点の中で,ψに入力枝ないし,出力枝を1本だけもつ点があるとする.もしその枝が入力枝であるとすれば,枝集合ρを含むハミルトンタイはその入力点を通るとき必ずその枝を通過しなくてはならないから,その入力枝は枝集合ρを含むハミルトンタイの枝集合に含まれる.同様のことはこの枝が出力枝の場合にも言える.
(4) 未検定枝集合ψに含まれる1本だけの入力枝ないし出力枝は確定枝集合ρを含むハミルトンタイに含まれる枝であり,この枝をρに付け加えた枝集合ρ' はGのハミルトンタイの枝集合である.
(5) ρ' をρに置き換えてこの操作を繰り返すことによって,枝集合ψが空になるか,ないし1本だけの入力枝ないし出力枝が無い状態に到達する.
この最後のステップで得られた枝集合ρ' の規定する検定全域グラフEが存在することは明らかである.ρ' はハミルトンタイの部分枝集合であるから,検定全域グラフEは検定ハミルトングラフである.よって,ハミルトングラフGのハミルトンタイに含まれる枝集合の部分集合ρがあるとき,ρを確定枝集合に含むグラフGの検定ハミルトングラフが存在する.
定理2-5.2: 検定短絡グラフ定理
ハミルトングラフGのハミルトンタイに含まれる枝集合の部分集合ρがあり,ρを確定枝集合とするGの検定ハミルトングラフをEとするとき,グラフEの検定短絡グラフSはハミルトングラフである.
証明:
定理2-5.1からグラフGのハミルトンタイに含まれる枝集合の部分集合ρがあるとき,ρを確定枝集合に含むグラフGの検定ハミルトングラフが存在する.ハミルトングラフEの未検定枝集合をψとし,ψを枝集合とする検定グラフEの部分グラフをE' とする.枝集合ρを含むGのハミルトンタイをΠとしΠの枝集合からρを除去した残りの枝集合を残余枝集合ξとする.ρを枝リストρiの集合{ρi}とし,ρiの始点と終点をそれぞれPi,Qiとするとき,検定全域グラフの定義より,
(1) ψにはρの枝の端点のうち,Pi,Qi以外の点に接続する枝は存在しない.
(2) ψにはPiを出力点とする枝は存在しない.
(3) ψにはQiを入力点とする枝は存在しない.
(4) ψにはQiを出力点とし,Piを入力点とする枝は存在しない.
よって,Eの部分グラフE' の上で,枝集合ρの枝リストρiの始点と終点を短絡しても,E' の枝数は変化せず,短絡点のラベルの相違を無視すればE' の枝とψの枝には完全な対応がある.すなわち,E' の上で枝集合ρの枝リストρiの始点と終点を短絡して得られるグラフをSとすれば,Sは検定グラフEの検定短絡グラフであり,特に,Gのハミルトンタイの残余枝集合ξと一対一に対応する枝集合ξ' が存在する.
ハミルトンタイΠの枝集合は枝集合ρと枝集合ξの合併である.ハミルトンタイΠについて枝集合ρの枝リストの始点と終点を短絡する操作を行った上で枝集合ρを除去すると,ハミルトンタイΠから枝集合ρを除去した分短縮されたGの初等的閉路Π' を得ることができる.このとき,閉路Π' の点と短絡グラフSの点は短絡点を含めて一対一に対応し,その点数は等しく,閉路Π' の枝集合はグラフS上の枝集合ξ' と完全に対応しているから,閉路Π' に対応するSの初等的閉路πが存在し,かつπはSの全域パスである.よってSにハミルトンタイが存在し短絡グラフSはハミルトングラフである.
定理2-5.3: 短絡グラフ法の原理
グラフGの部分枝集合ρがあり,ρを確定枝集合とするGの検定全域グラフEが存在するとき,グラフEの検定短絡グラフSが存在する.このとき,短絡グラフSがハミルトングラフであれば,グラフGはハミルトングラフである.
証明:
グラフEの枝集合ρの枝リストをとし,これに対応するEの検定短絡グラフS上の短絡点をとする.仮定によりグラフSはハミルトングラフであるから,SのハミルトンタイΠが存在する.短絡グラフS上の短絡点を切り開いて,枝集合ρの枝リストを挿入する操作を行なえば,SのハミルトンタイΠを枝集合ρの分だけ伸長した初等的閉路πを得て.これに対応する初等的閉路π' が検定グラフE上に存在する.
検定短絡グラフの定義から,枝集合ρの端点の集合と短絡グラフSの短絡点を除く点の集合を合併するとグラフEの点集合となることは明らかであり,閉路π上にはこれらの点がすべて存在していることから,検定グラフEの閉路π' の上にもグラフEのすべての点があるので閉路π' はグラフEのハミルトンタイである.
グラフEはグラフGの全域部分グラフであるから,グラフEのハミルトンタイはグラフGのハミルトンタイにほかならない.よって,グラフGはハミルトングラフである.
補題2-5.1: ハミルトンタイの存在証明
ハミルトングラフGのハミルトンタイに含まれる枝集合の部分集合ρがあり,ρを確定枝集合とするGの検定ハミルトングラフをEとするとき,グラフEの未検定枝集合に含まれる枝でグラフEの検定短絡グラフSの矛盾枝でない枝χとρを含むグラフGのハミルトンタイが存在する.但し,検定グラフEの未検定枝集合の枝と対応する短絡グラフSの枝において,短絡点のラベルによる相違は無視できるものとする.
証明:
グラフEの未検定枝集合をψとする.グラフEの検定短絡グラフSには検定ハミルトングラフEの未検定枝集合ψの枝に対応する枝がすべて含まれている.定理2-5.2より短絡グラフSはハミルトングラフであるから,グラフSの矛盾枝でない任意の枝を選び,これをχとするとき,χを含むSのハミルトンタイが存在する.このハミルトンタイの枝集合をξSとしたとき,グラフEには対応する枝集合ξEが存在し,かつ枝集合ξEと枝集合ρがグラフE上のハミルトンタイを構成することは明らかである.
グラフEはグラフGの全域部分グラフであるから,グラフEのハミルトンタイはグラフGのハミルトンタイにほかならない.よって,検定ハミルトングラフEの未検定枝集合に含まれる枝でグラフEの検定短絡グラフSの矛盾枝でない枝χとρを含むグラフGのハミルトンタイが存在する
補題2-5.2: 検定ハミルトングラフの存在証明
ハミルトングラフGのハミルトンタイに含まれる枝集合ρを確定枝集合とするグラフGの検定ハミルトングラフをEとするとき,グラフEの検定短絡グラフSの矛盾枝でない枝χとρを確定枝集合に含むGの検定ハミルトングラフが存在する.
証明:
補題2-5.2は定理2-5.1と補題2-5.1の結論から直接に帰着される.まず補題2-5.1から,ハミルトングラフGのハミルトンタイに含まれる枝集合ρがあり,ρを確定枝集合とするGの検定ハミルトングラフをEとするとき,グラフEの検定短絡グラフSの矛盾枝でない枝χとρを含むグラフGのハミルトンタイが存在する.よって,枝集合ρに枝χを追加した枝集合ρ' はGのハミルトンタイの部分枝集合であり,定理2-5.1よりρ' を確定枝集合に含むグラフGの検定ハミルトングラフが存在する.
■定理2-5.1から,グラフGがハミルトングラフであるときには,Gのハミルトンタイに含まれる枝集合の部分集合ρを確定枝集合に含むグラフGの検定ハミルトングラフが存在することが保証される.しかし,部分枝集合ρがハミルトンタイに含まれない枝(矛盾枝ないし障害枝)を含む場合,あるいはグラフGがハミルトングラフでない場合には,検定全域グラフを得られないことがある.これは既に因子検定の項で述べたデッドロックと呼ぶ現象の発生によるものである.
■検定全域グラフが得られたとしても,それは必ずしもその検定グラフが検定ハミルトングラフであることを意味しない.実際,矛盾枝ないし障害枝が確定枝集合に紛れ込んでいても,かなりの期間潜伏してデッドロックが発生しないということは有り得る.しかし,短絡グラフの再帰プロセスが進行していずれかの段階で極小のハミルトンタイを得ることができれば,原グラフがハミルトングラフであることは定理2-5.3によって保証される.極小のハミルトンタイと言えば,自己ループということになるが,短絡グラフ検定には自動確定のプロセスがあらかじめ組み込まれているので,通常はそれよりも早い段階で自動確定し,停止する.
■「枝集合ρを確定枝集合に含むグラフGの検定全域グラフEを求める」という操作は,「任意選択枝を含む枝集合ρを指定してグラフGの検定全域グラフEを求め,自動確定された確定枝集合ρ' を得る」という操作に当たるが,これを省略して「枝集合ρを確定して検定グラフEを得る」と表現する.またこのとき,自動確定された確定枝集合ρ' は枝集合ρによって返されるものとする.
■検定対象グラフGiを与えられたときの短絡グラフ法による全数検定の1ステージは以下のようなプロセスとして実行される.
(1) ρi=φを確定してグラフGiの検定グラフEiを得る.
(2) もし,Eiが得られなければGi=非ハミルトングラフで復帰する.
(3) もし,ρiがGiのハミルトンタイならばGi=ハミルトングラフで復帰する.
(4) Gi上の任意の点Piを選択し,Piのすべての枝bjについて以下を行なう.
(4.1) ρ=ρi∪bjとする.
(4.2) 枝集合ρを確定して,検定グラフEiを得る.
(4.3) もし,Eiが得られなければ次の枝に進む.
(4.4) もし,ρがグラフGiのハミルトンタイならばGi=ハミルトングラフで復帰する.
(4.5) 検定グラフEiの短絡Siグラフを求める.
(4.6) 短絡グラフSiを検定対象グラフGi+1として短絡検定を再帰実行する.
(4.7) Gi+1=ハミルトングラフならば,Gi=ハミルトングラフで復帰する.
(5) Gi=非ハミルトングラフで復帰する.
■定理2-5.3は短絡グラフ法で再帰的に検定を下降して行ったとき,もっとも小さい短絡グラフでハミルトンタイを得ることができれば,原グラフがハミルトングラフであることが立証されるという意味で,短絡グラフ法の原理ともいうべきものであるが,さらにハミルトン性を保存するグラフ変換の方法を示唆するものであるとも言える.グラフGから検定グラフEを経て,短絡グラフSを求める操作をある種の位相同型な短絡縮約を伴うグラフ変換と捉えることは可能であり,この短絡縮約操作は原グラフのハミルトン性を保存する.
定理2-5.3が成立することの利点はこればかりではない.これまでに因子検定の弱点を補強すべき各種の検定法について述べてきたが,これらを因子検定のある段階に押し込むような方法で実装しようとしたら,検定の一貫性や正当性を保証することは著しく困難なものとなったであろうことは疑うべくもない.ところが,定理2-5.3により検定のすべての段階をハミルトン検定そのものとして行なうことが可能となったのだから,この定理が与えられたことの意義は大きい.これら各種検定と因子検定を統合することの論理的正当性と実装上の実現可能性がこの定理によって始めて確立され,ハミルトン検定が終結可能であるという展望が切り開かれた.