④
直列ブリッジ（２つの確定枝の２端点を接続する枝と対角点を結ぶ枝からなる舛目図形）の辺となる枝．対角点を結ぶ枝は自動確定される．２－４．直並列検定
■グラフ中に並列的な要素があると非ハミルトングラフになるであろうことは直感的に理解されるが，グラフ理論で言う直並列位相同型の概念では，ハミルトングラフと非ハミルトングラフを分離することができないので，ハミルトン位相同型を判定できるような簡約手続きを開発した．直列枝はハミルトン検定上では必ず確定パス上の枝となるものであるから，同型変換した後も直列枝であることが属性として保存され，判別可能であることが必要である．ここでは直列枝という属性を持った特殊な枝を導入して，この要件を満足することにする．
■ハミルトン直並列簡約とは以下のような手続きである．
(1) 直列した枝を短絡，除去して１本の直列枝属性を持った確定枝に変換する．
(2) 確定枝の端点以外の点を短絡する．
(3) 直列枝ないし，確定枝と直列する枝が無くなるまで，(1)から繰り返す．
■直並列変換はつまるところ３因子以上の点をすべて短絡縮約して，グラフ上の２因子ベクトルを検査する手法である．確定パスを確定枝と同一視することは可能だから，この検定は検定途上にある確定パスとグラフの未検定部分との全域的な関係を抽出するものと見ることもできるだろう．このようにして得られた簡約グラフが次のいずれかである場合，原グラフは非ハミルトングラフである．
① 直列ループ：ハミルトンタイではない確定枝のみの閉路が存在する．
② ３並列直列：１点を共有する３本の確定枝が存在する．
■直並列検定は本質的に無試行判定であるが，直列ループと３並列直列の２つの相を非ハミルトングラフとして分離することができる．①はハミルトン公準の１閉路規則違反であり，②は２因子規則違反であるが，因子検定がこれらを検出できるよりもずっと早期に検出できる可能性がある．また，直並列検定はその副産物として，直列枝に関る矛盾枝ないし障害枝を検出する．直並列検定により無試行判定で除去できる矛盾枝ないし障害枝には以下がある．
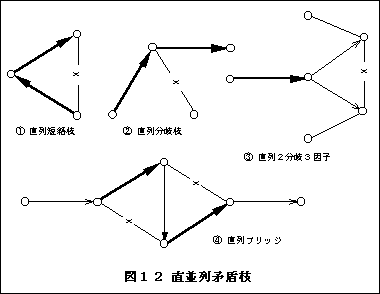
① 確定枝に並列する枝，ないし隣接する確定枝の２端点を接続する枝
② 隣接する確定枝の接続点に接続する枝
③ 直列２分岐３因子点を接続する枝（確定枝の端点に２分岐する枝があり，その２つの枝の端点がともに３因子点であるとき，それらの点を接続する枝）
④
直列ブリッジ（２つの確定枝の２端点を接続する枝と対角点を結ぶ枝からなる舛目図形）の辺となる枝．対角点を結ぶ枝は自動確定される．
■このうち，③は３端子分割検定によっても処理可能であり，④は２端子分割で処理することができるので，①，②以外は必須機能ではない．この種の一種の定石のようなものを検定に組み込んでゆくことになるとすれば，ハミルトン検定はおそらく囲碁の必勝プログラムのようなものになってしまうかもしれない．検定プログラムの実用性能を向上させるという理由からであれば，そのような逸脱が場合によっては許容されることもあるだろう．
■直並列検定は早期に矛盾を検出できる能力を持った有力な方法ではあるが，原理的に，グラフ上に２因子が少なくとも２箇所以上無ければ効力を持たない．直並列検定を拡張して，確定パス上の単独枝を含む枝リストを一本の確定枝とみなしてよいということにすれば．枝を確定する操作が直ちに直並列検定に反映されることになるだろう．
■また，確定パスの出発点をグラフ上に分散して３定点観測するというような方法も考えられる．グラフ上に確定枝が３本分散して配置されている場合，直並列位相変換で得られるグラフは次の6種の原始文字グラフのいずれかになるものと考えられる．（３枝以上では，さらにいくつかの原始文字が追加されることになるだろう．）
■ハミルトン直並列簡約を正当化する定理は現在のところ，まだ証明を得るに至っていない．位相同型変換の証明は一般に困難なものであることが多いのだが，特にこの証明はかなりの難関であるように思われる．４色定理問題の証明のような込み入ったものになることをおそれている．
定義2-4.1： ハミルトン直並列簡約，ハミルトン直並列
以下のグラフ変換をハミルトン直並列簡約と呼ぶ．①枝数２の点を除去して１本の確定枝とする．②確定枝の端点でない隣接する枝数３以上の点を短絡縮約する．③これらを繰り返して操作できる点がなくなったら，確定枝でない枝をすべて解放除去する．④つぎに，任意の閉路に含まれないすべての確定枝を解放除去する．
グラフＧにハミルトン直並列簡約を行なうことにより，以下のグラフのいずれかと同型なグラフを部分グラフとして持つようになるとき，このグラフはハミルトン直並列であると言う．
ａ．孤立点を真部分グラフとして含むグラフ
ｂ．２点３重枝グラフ（並列枝を３本持つ２点グラフ）
定理2-4.1: ハミルトン直並列グラフ
ハミルトン直並列であるようなグラフは非ハミルトングラフである．
証明： 証明は保留する．
