2-5. Short-circuit graph Method

Short-circuit graph method gives more rigid formalism to the factor experiment we have recited so far and it institutes a base of Hamiltonian experimentation. In short-circuit experiment method, we proceed experiments with a method to compose a reduced graph short-circuiting points on determinative paths in each experiment stage and to inquire again a Hamiltonian tie on the graphs. That is, the short-circuit method is a completely recursive experiment process and halts when a Hamiltonian tie is obtained. In the case that we cannot get a resolution after examining every node of a search tree of N - 1 height, we concludes that is a non-Hamiltonian graph.

In short-circuit graph method, we experiment using 2 kind of peculiar graph of experimental spanning graph and experimental short-circuit graph. At first, we prove theorems regarding these two graphs and show that this experiment method is adequate. Hereinafter, we regard a Hamiltonian graph as a directed graph with Hamiltonian ties. And also, we assume all of graphs are directed and connected.

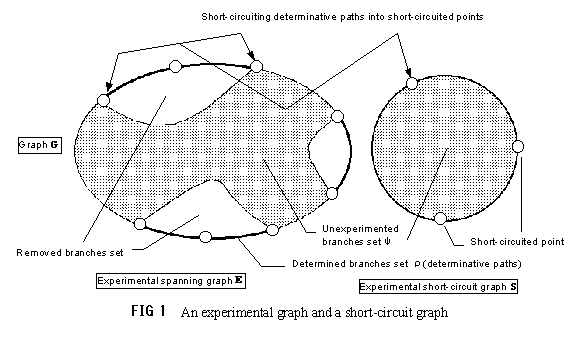
Def.2-5.1 determined branches set of experimental spanning graph

We say that a determined branches of experimental spanning graph of graph G is a set of branches not owning input points or output points of graph G jointly and also not containing such a branch as connect the end point and the start point of branches list consist of adjacent branches of the branches set.

Def.2-5.2 experimental spanning graph

We say that an experimental spanning graph E of graph G is a subgraph including every points of graph G, and also is a graph with branches set of an union of determined branches setand unexperimented branches setof graph G prescribed by, where includes a plurality of input branches of input points and output branches of output points of branches included in when unexperimented branches set is not empty. Where unexperimented branches set is a subset of branches set of graph G, and also is a remainder branches set obtained by removing all branches of determined branches set , input branches of input points and output branches of output points of all branches of and such branches that incident from end point to start point of branches lists connecting adjacent branches in from branches set of G. From the definition, experimental spanning graph is a spanning subgraph of graph G.

Def.2-5.3 experimental Hamiltonian graph

An experimental Hamiltonian graph of graph G is such an experimental spanning graph of G that it's determined branches set is subsetof branches set of Hamiltonian tie of graph G. Experimental Hamiltonian graph does not include contradictory branches from definition.

Def.2-5.4 experimental short-circuit graph

Let experimental spanning graph of graph G be E. An experimental short-circuit graph S of G is a graph obtained by short-circuiting end point and start point of all of branches lists of determined branches setin such a subgraph of E that it's branches set is unexperimented branches set . Branches set of S includes all of branches of neglecting the differences of labels of short-circuited points.

Theorem 2-5.1. existence theorem of experimental Hamiltonian graph

When there exists a subset of branches set included in a Hamiltonian tie of Hamiltonian graph G, there exists an experimental Hamiltonian graph of G including in it's determined branches set.

Proof.

Since is a branches subset of a Hamiltonian tie, it does not contain such branches as own input points or output points of G jointly. And also it does not contain such branches as incident from end point to start point of branches list consist of adjacent branches of the branches set.

We can compose determined branches set' containing branches set and unexperimented branches set prescribed by ' with the following procedure.

(1) Let be branches set ' = . Let branches subset obtained by removing branches set ' from branches set of graph G be and let subgraph of G with branches set of union of ' and be G'.

(2) Remove all of input branches of input points and output branches of output points of each branches of '. Further, if there exist branches incident from end point to start point of branches lists of ', remove them in the same way.

(3) If there exists a point of each points of G' with either singular input branch or singular output branch, move the point from to '.

(4) Repeat from (2) until there is no points having either singular input branch or singular output branch in .

In graph G' generated in such way, since there exist determined branches set' and unexperimented branches set prescribed by ' and if the unexperimented branches set is not empty, there exists a plurality of input branches of input points and output branches of output points of branches contained in , therefore G' is an experimental spanning graph of graph G. Said step (2) corresponds to a step of determination in factor experiment. If we can formalize an algorithm of one step and make an assurance that branches set ' progressed one step is always a subset of branches set of Hamiltonian tie, it is proved that finally obtained experimental spanning graph is an experimental Hamiltonian graph. We will show this below.

(1) Let be a branches subset of Hamiltonian tie of Hamiltonian graph G. Let branches subset obtained by removing from branches set of graph G be and let subgraph of G with branches set of union of and be G'.

(2) Remove all of input branches of input points and output branches of output points of each branches of from . Further, if there is a branch incident from end point to start point of branches lists of , remove in the same way. These branches are such branches as not included in a Hamiltonian tie including branches set.

(3) Since G has a Hamiltonian tie and branches set is a branches subset of a Hamiltonian tie, branches set includes all of branches not included in branches set of Hamiltonian tie including . Suppose that in each points of G' there are points having either singular input branch or singular output branch of branches set. If the branch is an input branch, since Hamiltonian tie including branches set must pass through the branch when it pass the input point, the input branch is contained in branch set of Hamiltonian tie including branches set. The same is true in the case that this is an output branch.

(4) Either singular input branch or singular output branch contained in unexperimented branches set is a branch included in Hamiltonian tie including determined branches set, and branches set' obtained by adding this branch to is a branches set of Hamiltonian tie of G.

(5) Repeating this operation with replacing ' with , we reach to the state that branches set turns to be empty or there is neither singular input branch or singular output branch.

It is obvious that there exists experimental spanning graph E prescribed by branches set' obtained in this last step. Since' is a branches subset of Hamiltonian tie, the experimental spanning graph E is an experimental Hamiltonian graph. Hence when there exists a subsetof branches set included in a Hamiltonian tie of Hamiltonian graph G, there exists an experimental Hamiltonian graph of G including in it's determined branches set.

Theorem 2-5.2 experimental short-circuit graph

When there is a subset of branches set included in a Hamiltonian tie of Hamiltonian graph G and let such an experimental Hamiltonian graph as it's determined branches set is be E, experimental short-circuit graph S of graph E is a Hamiltonian graph.

Proof.

From theorem 2-5.1, when there exists a subset of branches set included in a Hamiltonian tie of Hamiltonian graph G, there exists an experimental Hamiltonian graph of G including in it's determined branches set. Let unexperimented branches set of Hamiltonian graph E be and let such subgraph of experimental graph E that it's branches set is be E'. Let a Hamiltonian tie including branches set be and let branches set remained by removing from branches set of be remainder branches set. Let be branches lists {i}, let start points, end points be Pi, Qi respectively, when from the definition of experimental spanning graph,

(1) In not exists such a branch as connects to points except Pi, Qi of terminal points of branches of
(2) In not exists such a branch as it's output point is Pi
(3) In not exists such a branch as it's input point is Qi
(4) In not exists such a branch as it's output point is Qi and it's input point is Pi

Therefore, even if we short-circuit the start point and the end point of branches list i of branches set on subgraph E' of graph E, branches number of E' does not change and there exists complete correspondence between a branch of E' and a branch of neglecting the differences of labels of short-circuited points. That is, let a graph obtained by short-circuiting a start point and an end point of branches list i of branches set on E' be S, S is an experimental short-circuit graph of experimental graph E, particularly there exists such a branches set ' as one to one corresponds with remainder branches set of Hamiltonian tie of G.

Branches set of Hamiltonian tie is an union of branches setand branches set. With respect to Hamiltonian tie, after the operations of short-circuiting a start point and an end point of branches lists of branches set, remove branches set then we obtain an elementary circuit' of G shortened by the degree of removing branches set from Hamiltonian tie. When points of circuit' corresponds one to one with points of short-circuit graph S including it's short-circuited points, their points number is equal and further branches set of circuit' corresponds completely with branches set' on graph S', therefore there exists elementary circuit of S and is a spanning path of S. Hence there exists a Hamiltonian tie in S and short-circuit graph S is a Hamiltonian graph.

Theorem 2-5.3 Principle of Short-circuit graph Method

When there is a branches subset of graph G and there exists such an experimental spanning graph E as is it's determined branches set, there exists an experimental short-circuit graph S. Where if short-circuited graph S is a Hamiltonian graph, graph G is a Hamiltonian graph.

Proof.

Let a branches list of branches set of graph E be i, short-circuited point on experimented short-circuit graph S of E corresponding to i be Pi. By the premise, graph S is a Hamiltonian graph then there exists a Hamiltonian tieof S. If we make an operation to incise a short-circuited point Pi on short-circuit graph S and insert a branches list i of branches set, we obtain an elementary circuit made by expanding Hamiltonian tie of S by the degree of branches set and there exists an elementary circuit' corresponds to on the experimental graph E.

From the definition of experimental short-circuit graph, it is obvious that an union of terminal points set of branches set and points set of short-circuit graph S excepting short-circuited points, and since there exist all of these points on circuit, there also exist all of the points of graph E on the circuit' of experimental graph E, hence circuit' is a Hamiltonian tie of graph E.

Since graph E is a spanning subgraph of graph G, a Hamiltonian tie of graph E is nothing else than a Hamiltonian tie of G. Hence graph G is a Hamiltonian graph.

Lemma 2-5.1 Existence assertion of Hamiltonian tie

Suppose there exists a subset of branches set included in Hamiltonian tie of Hamiltonian graph G. Let such experimental Hamiltonian graph of G as it's determined branches set is be E. When there exists a Hamiltonian tie of G including both of and such branch as contained in unexperimented branches set of graph E and also not a contradictory branch of experimental short-circuit graph S of graph E. Provided that in such branches of short-circuit graph S as corresponds to branches of unexperimented branches of experimental graph E, differences by labels of short-circuit points can be neglected.

Proof.

Let unexperimented branches set of graph E be. In Experimental short-circuit graph S includes all of the branches corresponding to branches of the unexperimented branches set of graph E. From theorem 2-5.2, short-circuit graph S is a Hamiltonian graph then select such an arbitrary branch as not a contradictory branch of graph S and let this branch be, when there exists a Hamiltonian tie of S including. When let branches set of this Hamiltonian tie be S, it is obvious that there exists branches set E corresponding to S in graph E and branches set E and branches set constitute a Hamiltonian tie on graph E.

Because graph E is a spanning subgraph of G, a Hamiltonian tie of E is nothing else than a Hamiltonian tie of graph G. Hence there exists a Hamiltonian tie of graph G including and such branch as not a contradictory branch of experimental short-circuit graph S of graph E.

Lemma 2-5.2 Existence assertion of experimental Hamiltonian graph

When let such an experimental Hamiltonian graph of G as it's determined branches set is branches setincluded in a Hamiltonian tie of Hamiltonian graph G be E, there exists an experimental Hamiltonian graph of G with a determined branches set including and such branch as not a contradictory branch of experimental short-circuit graph S of graph E.

Proof.

Lemma 2-5.2 is concluded from the results of theorem 2-5.1 and lemma 2-5.1. First, suppose that there exists a branches set included in a Hamiltonian tie of Hamiltonian graph G and let such an experimental Hamiltonian graph as it's determined branches set is be E, when there exists a Hamiltonian tie of graph G including and such branch as not a contradictory branch of experimental short-circuit graph S of graph E. Hence branches set' made by adding branch to branches set is a branches subset of a Hamiltonian tie of G and from theorem 2-5.1, there exists an experimental Hamiltonian graph of graph G with determined branches set including'.

From theorem 2-5.1, it is assured that when graph G is a Hamiltonian graph, there exists an experimental Hamiltonian graph of graph G with determined branches set including subset of branches set included in a Hamiltonian tie of G. However, Either in the case that branches subsetincludes branches not included in a Hamiltonian tie (contradicted branches or obstacle branches) or in the case that graph G is not a Hamiltonian graph, there happens that we cannot obtain an experimental spanning graph. This is owing to an occurrence called deadlock which we already mentioned in the section of Factor Experiment.

Even though we obtain an experimental spanning graph, it does not necessarily mean that the experimental graph is an experimental Hamiltonian graph. Actually, even if a contradictory branch or an obstacle branch has mingled in a determined branches set, it is probable that a deadlock does not occur for a mean while in latency. However, if we obtain a minimal Hamiltonian tie in any phase progressing the recursive process of short-circuit graphs, theorem 2-5.3 gives an assurance that the original graph is a Hamiltonian graph. Concerning the minimal Hamiltonian tie, it might mean a self-loop but ordinarily it goes auto-determined and stops at earlier stage than that.

An operation "Inquire an experimental spanning graph E of graph G with determined branches set including branches set" corresponds to an operation "Designating branches setincluding arbitrary selected branches, inquire an experimental spanning graph E of graph G and obtain determined branches set' auto-determined" , but we abbreviate this and represent as "Determine branches set and obtain experimental graph E". Further, when we consider that determined branches set' auto-determined shall be returned with branches set.

One stage of thorough examination in all numbers by short-circuit graph method with objective graph Gi given for the stage is executed as a process below.

(1) Determinei =and obtain experimental graph Ei of graph Gi.
(2) If fail to obtain Ei then return with Gi =non-Hamiltonian graph.
(3) If i is an Hamiltonian graph of Gi then return with Gi=Hamiltonian graph.
(4) Select an arbitrary point Pi on Gi and dispose of all of branches bj of Pi as below.

(4.1) let be=i bj
(4.2) Determine and obtain experimental graph Ei
(4.3) If fail to obtain Ei then proceed to next branch.
(4.4) If is a Hamiltonian tie of graph Gi then return with Gi=Hamiltonian graph.
(4.5) Inquire the short-circuit graph Si of experimental graph Ei.
(4.6) Execute short-circuit experiment recursively with Si as objective graph Gi+1
(4.7) If Gi+1=Hamiltonian Graph then return with Gi=Hamiltonian graph.

(5) Return with Gi=non-Hamiltonian graph.

In the meaning that when we descend recursively with short-circuit graph method, if we obtain a Hamiltonian tie in the minimum short-circuit graph, it is assured that the original graph is a Hamiltonian graph, the theorem 2-5.3 is so to say a principle of short-circuit method, furthermore it might be said that it suggests a graph conversion method to preserve Hamiltonicity. It is able to consider that an operation to inquire short-circuit graph S from graph G via experimental graph E is a graph transformation with a kind of homeomorphic shortening and reduction, and this operation of shortening and reduction preserves the Hamiltonicity of the original graph.

The merit that the theorem 2-5.3 holds is more than this. We have recited several experiments to reinforce deficiency of the factor experiment but it is doubtless that if we try to implement them in the manner to push them into some stage of factor experiment, to assure the consistency or the justness of experiments must be remarkably difficult.

However, for we come to be able to proceed all of stages of experiments as the Hamiltonian experiment itself with the theorem 2-5.3, the significance to be given this theorem is great. Due to this theorem, the logical justification to integrate these experiments and factor experiment or the practical possibility with respect to the implementation have established for the first time and the view that Hamiltonian experimentation can be completed has been cut out.