2-4. Series-Parallel Experiment

Although it is intuitively understood that a graph having parallel elements turns to be a non-Hamiltonian graph, the concept of series-parallel homeomorphism cited in Graph Theory cannot separate non-Hamiltonian graph from Hamiltonian graph, then we developed such conversion method to judge Hamiltonial homeomorphism. As series branches are always to be branches on determinative paths in Hamiltonian experimentation, it is necessary that the attribute of being series branches must be preserved to be distinguished later. Here, we introduce a peculiar branch having series branch attribute to satisfy this condition.
Hamiltonial series-parallel reduction is such a procedure below.

(1) Replace series branches with a determined branch of series branch attribute.
(2) Short-circuit other points than terminal points of determined branches.
(3) Repeat from (1) until there is no series branches or branches serial to determined branches.

To be short, serial-parallel reduction is a method to short-circuit all of 3 or more-factor points and to examine 2-factor vectors on a graph. As it is possible to identify determinative paths with determined branches, we may consider this experiment that it extracts global relation among determinative paths on the way of experiments and a part of graph not yet experimented. If a reduced graph obtained in such way is one of the case bellow, the original graph is a non-Hamiltonian graph.

(1) series loop: There exists a circuit which is not a Hamiltonian tie.
(2) 3-parallel-series: There exist 3 determined branches share one point.

Series-parallel experiment is essentially a judgment with non-retrial and it is able to separate both model of series loop and 3-parallel-series as non-Hamiltonian graph. (1) is an offense against 1-circuit rule of Hamiltonian postulate and (2) is an offense against 2-factor rule, and here is a possibility to detect earlier by far than factor experiment become able to detect them. Moreover, series-parallel experiment can detect contradictory branches or obstacle branches with respect to series branches as by-products. Contradictory branches and obstacle branches to be removed by series-parallel experiment are the followings.

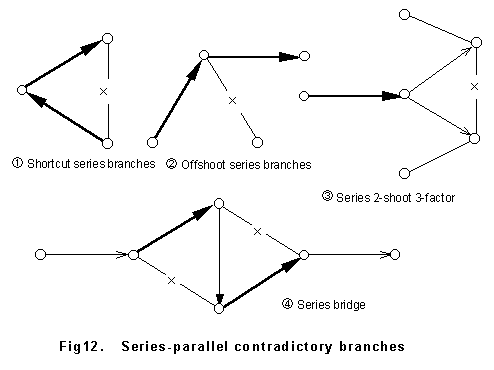
(1)A branch parallel to determined branch or a branch conjoining 2 terminal points of adjacent determined branches
(2)A branch connected to the joint point of adjacent determined branches
(3)A branch conjoining series 2-shoot 3-factor points (there exist 2 shoot branches at a terminal point of a determined branch and end points of the 2 shoot branches are both 3-factor point, when the branch conjoin those points )
(4)Branches being 2 edges of a series bridge (a square figure comprising branches conjoining 2 terminal points of 2 determined branches and a branch conjoining diagonal points) , a branch conjoining diagonal points shall be auto-determined.

Among them, we can manage (3) with 3-terminal division experiment and (4) can be disposed by 2-terminal experiment, therefore the others than (1) and (2) are not indispensable functions. If we would feature such a kind of formulas in go-game in the experiments, Hamiltonian experimentation should probably be something like a sure-victory program of go-game. Owing to a reason to improve practical efficiency of experimental program, those deviation might be admitted in some cases.

Although series-parallel experiment is a superior method with an ability to detect offenses in an early stage, principally it has no efficiency for such graphs as have 2-factor points at less than 2 places. Expand the series-parallel experiment and admit that a branches list or a single branch on determinative paths may be regard as a determined branch, an operation to determine a branch shall be reflected directly to the series-parallel experiment.

And also, we can suppose such a method as dispersing start points of determinative paths on the graph and observing at 3 fixed points . In the case that 3 determined branches are disposed on the graph dispersively, it is considered that a graph obtained by series-parallel experiment comes to be one of the 6 kinds of primitive letter graphs below. (Above 3 branches, still more primitive letters would be added. )

At the present time, a theorem to justify Hamiltonian series-parallel experiment has not come to obtain it's proof yet. While to prove homeomorphic conversion is generally difficult, this proof especially seems fairly hard. We are afraid that it comes to be such involved one as a proof of 4-color-theorem problem.

Def.10 Hamiltonian series-parallel reduction, Hamiltonial series-parallel

We call the following graph conversion by Hamiltonian series-parallel reduction.

• Remove such points that branches number equal 2 and make one determined branch.
• Short-circuit adjacent points of more than 3 branches number except terminal points of determined branches.
• Repeat these operations. When there is no point to be disposed, open-cut every branches except determined branches.
• Next, Open-cut every determined branches not included in any circuits.

As the result of this Hamiltonian series-parallel reduction with graph G, if the graph comes to have a subgraph of isomorphic graph represented below, we say this graph is Hamiltonial series-parallel.

a. a graph contains an isolate point as a proper subgraph.
b. 2-point 3-mult-branch graph (2 points graph having 3 parallel branches)

Theorem 4. Hamiltonial series-parallel graph

A Hamiltonial series-parallel graph is a non-Hamiltonian graph.

Proof.

Pending.