1-3. There Are k-Terminal Division Difficult Graphs

Mesh-diagram experiment became the first method to detect a non-Hamiltonian graph with judgment with non-retrial and the direct motive to develop that method was a fact that there were k-terminal division difficult graphs. So to say, on k-terminal division, the cost to confront determinative paths of left and right subgraphs came k! for terminal points number k then the cost became almost N! for large number of k. Since k-terminal divisions are executed recursively, for the sake of making a k-terminal division of a graph, to make the least k-terminal division is enough, and so a k-terminal division difficult graph is a graph where the value k giving the least k-terminal division of the graph is above some constant value i.e. 20.

A mesh graph is exactly an example of such a graph. For instance, in the case of m*m mesh graph, points number becomes N = m^2 and the terminal division crossing the graph vertically or horizontally comes to k= then the graph is k-terminal division difficult. (In the case of a square-mesh graph, there might be less k-terminal points at the corners of the diagram then small k-terminal divisions might be progressed like biting an apple, but there are completely k-terminal division difficult graph in mesh graphs.) Since k-terminal division experiment was a strong method of extremely rapid convergence, there was no way than considering other tactics for those graphs which were too hard for the strategy.

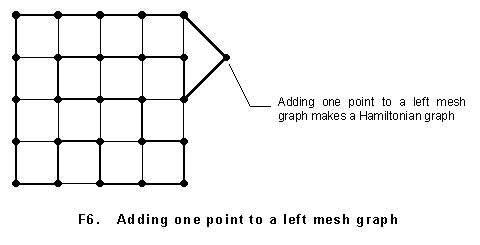
In the aspect of graphic topology, it might be appropriate to regard the value k giving the least k-terminal division is a shorter diameter of the graph. In other words, a k-terminal division difficult graph is such a type of graph as large round the waist, stumpy and plump. A normal right mesh graph (an even number points mesh graph with no lack of branches) must be a Hamiltonian graph. Although a left mesh graph is a non-Hamiltonian graph, it can be changed to a Hamiltonian graph adding or removing arbitrarily one point and converting it into an even number points graph. In view of k-terminal division experiment, a mesh graph is enormously difficult graph but it turns unexpectedly to be an easy graph when it appears on a mesh-diagram.

An experiments method to use together with three kinds of experiment of series-parallel experiment, mesh-diagram experiment and k-terminal division experiment is called three modes experiment. Each three kinds of experiment can separate a non-Hamiltonian graph with its own judgment rule. Very small some parts of graphs are judged to be non-Hamiltonian graphs by all of three kinds of experiments. Some graphs receive judgment being a non-Hamiltonian graph from two experiments. But there also exist non-Hamiltonian graphs which is disable to be separated by any experiment. For series-parallel experiment and mesh-diagram experiment have judgments with non-retrial, they can judge instantly. As k-terminal division experiment is a method who experiments recursively divided graphs, it is impossible in principle to judge instantly. A diamond figure is able to be judged at once and this is an possible exception of judgment with non-retrial of k-terminal division experiment.