1-2. A Graph without Hamiltonian Circuit

To make perfect k-terminal division and cut-set experiment was expected to nearly stop leaking through the mesh but in the face of the dilemma that was nonrealistic for the cost, the situation seemed almost impossible to break through. However, we became aware of a strange matter investigating k-terminal points subgraphs IO. That is, it came into question that there might be a peculiar figure class and a graph in which buried one of those figures became necessarily a non-Hamiltonian graph. If there are such figures, they should be called devil's diagrams. Under theoretical consideration, the probability of existence of such graphs seemed enough. We found a group of figures having such characteristics and gave it the name of diamond figure.

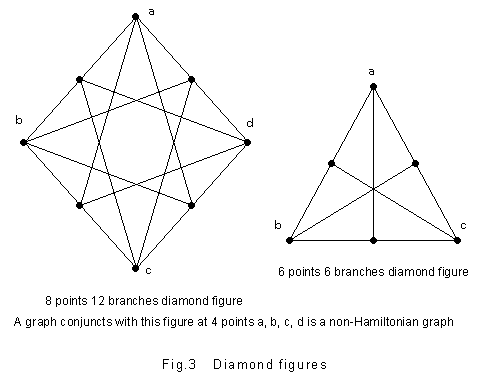
Whether a graph has a Hamiltonian circuit or not is a problem regarding the global characteristics of the graph and it cannot be judged in general by only it's local information. Actually, adding some points and branches to a non-Hamiltonian graph makes the graph a Hamiltonian graph, and adding still more makes a non-Hamiltonian graph again. However, in the case of diamond figure, a graph in which buried the figure become a non-Hamiltonian graph without exception. The characteristic of this figure is absolutely peculiar in the meaning that even if it is very small like a pin's head in an enormously big graph, it makes the whole graph a non-Hamiltonian graph.

The discovery of diamond figure brought us, completely fallen into blockade situation, to a great turning point. It showed us concretely the first example of a graph without Hamiltonian circuit. Owing to it, a hope that it might be probably possible to judge non-Hamiltonian graph without thorough examination in all numbers was born to us.

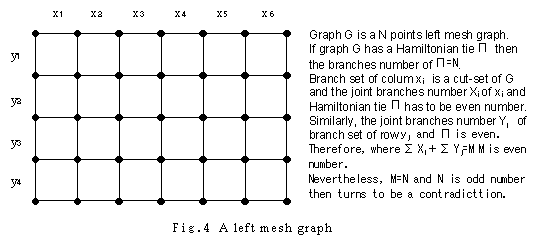
A typical non-Hamiltonian graph found in succession of (a graph in which buried) the diamond figure is a graph called left mesh graph or odd points mesh graph. We call a graph like a go-game board comprising squares or meshes by mesh graph here. As a go-game board has 19 rows -19 columns, it is a 361 points graph and the number of the points is odd then it is a left mesh graph. That a left mesh graph is a non-Hamiltonian graph can be proved easily using that cut-set IO of the graph must be even number*.

Due to the consideration of the left mesh graph, mesh-diagram experiment was introduced as the first method to judge being a non-Hamiltonian graph with non-retrial. In mesh-diagram experiment, two kinds of numbers called points score and branches score are calculated and some range of graphs can be judged to be non-Hamiltonian graphs with constraint inequalities conforming these variables.

Existence theorem of Hamiltonian Circuit is one of the basic theorems with respect to Hamiltonian Circuit Problem. This theorem shows a graph whose sum of branch numbers of any two points is more than N is a Hamiltonian graph. When such graph can be called a dense graph, a sparse graph can be concerned in contrast with the former. Naturally, it shall be expected that "a sparse graph is a non-Hamiltonian graph" and actually the below is concluded from the mesh-diagram experiment. "A graph where points number of its independent set is greater than N / 2 is a non-Hamiltonian graph". Independent set is a set of points two of which are not adjacent to each other and this shows that a graph where a half of its points are estranged from each other is a non-Hamiltonian graph.

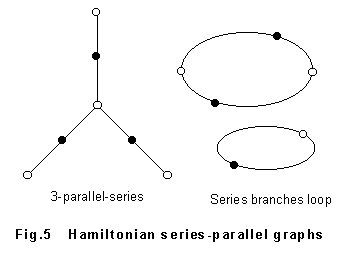
Series-parallel experiment was developed as one more method which can "judge being a non-Hamiltonian graph with non-retrial". Series branches are connected two branches with no cleavage and the connection point is a 2-factor point (a point that branches number is 2). Branches of 2-factor (point) are always branches on a Hamiltonian tie, then series branches are by all means included in a Hamiltonian tie. Series branches existing in a graph is in this meaning are the important factor to decide a topology of the graph and series-parallel experiment makes a non-Hamiltonian graph judgment with non-retrial using this fact.

Series-parallel experiment can separate both kind of graph as non-Hamiltonian graph, (1) a graph including a circuit comprising merely series branches, (2) a 3-parallel-series graph (a graph where 3 series branches share one point) . k-Terminal division or cut-set division separates non-Hamiltonian graphs like series-parallel contradiction. It is the case when a subgraph divided with k-terminal division shall be k-terminal divided again. As mentioned above, a graph where buried a diamond figure is detected as an IO contradiction of k-terminal division. Similarly, graphs detected IO contradiction with k-terminal division and cut-set division are all non-Hamiltonian graphs.

* Another proof of the non-Hamiltonian theorem of left mesh graph: Generally a mesh graph is called a grid graph or rectangular graph. It is easy to see that a gird graph is 2-colorable, hence bipartite. While an odd bipartite graph has no perfect matching and of course non-Hamiltonian. It comes from a simple observation that since the graph is odd, the size of upper part cannot be the same with the lower part. As well the opposite side is provable, i.e., an even grid graph, or a grid graph of either rows or columns is even,  is always Hamiltonian. A hint for proof: You can easily partition a grid graph with even vertices into a union of even cycles and find a pair of edges to bridge each pair of cycles. It seems that the Hamiltonicity of even grid graphs was first discovered in 1990 by Skiena.[SK]