An Efficient Factoring Algorithm by Repunit Number Method
Baba Laboratory
Michiro Nasu
Excerpt from theory-edge
Questions:
Propositions:
Definitions:
No.01: 2005-03-03 06:49:24 +0900 A Number
Puzzle
No.02: 2005-03-03 14:32:46 +0900 Reply to
Richard
No.03: 2005-03-03 14:52:16 +0900 Reply to
Max
No.04: 2005-03-03 22:31:46 +0900 Seven
Propositions
No.05: 2005-04-04 04:38:16 +0900 Proof of Proposition [8], prime repunits
No.06: 2005-03-05 02:12:15 +0900 False
answer to Question (4)
No.07: 2005-03-05 13:53:37 +0900 Reply to
Daniele wrt an online book
No.08: 2005-03-05 19:28:51 +0900 Apology to
Daniele
No.09: 2005-03-05 19:41:03 +0900 Proposal of
a Primitive Algorithm for factoring
No.10: 2005-03-07 01:34:35 +0900 Proposal of
a Systematic Method for factoring
No.11: 2005-03-07 22:58:05 +0900 Reply to
Richard
No.12: 2005-03-08 06:15:37 +0900 Proof of Proposition [8'], [10] and Proposal [9]
No.13: 2005-03-09 08:32:59 +0900 Analysis of
Repunit Table for primality condition
No.14: 2005-03-10 02:48:46 +0900 Reply to
Daniele
No.15: 2005-03-10 03:09:22 +0900 Self Answer
for the previous mail
No.16: 2005-03-10 04:47:42 +0900 Apology to
Daniele
No.17: 2005-03-11 06:10:34 +0900 Reply to
Vladmir
No.18: 2005-03-14 07:36:45 +0900 Reply to
Richard
No.19: 2005-03.15 12:14:01 +0900 Reply to
Daniele's 1st Proposal
No.20: 2005-03.16 12:27:43 +0900 Reply to
Daniele's 2nd Proposal
No.21: 2005-03.16 22:58:00 +0900 Reply to
Daniele's Answer
No.22: 2005-03.19 01:49:29 +0900 Proof of Proposition [15],[16] and [17]
No.23: 2005-03.20 10:47:59 +0900 Reply to Daniele's 3rd Proposal
No.24: 2005-03.24 12:11:48 +0900 Schoolgirl's Homework Conjecture, [9"] and [18]
No.25: 2005-03.25 16:42:03 +0900
Totient/u-length function graph (chart)
No.26: 2005-03.26 12:47:32 +0900 Proposal of
Lemma [19]
No.27: 2005-03.27 18:38:15 +0900 Reply to
Daniele, Reinvention of a wheel
No.28: 2005-03.30 13:41:16 +0900 Laglange's Theorem, Proposal P1-P7
No.29: 2005-04.02 13:41:16 +0900 Burton's
1989 Paper on primitive roots
No.30: 2005-04.13 03:14:19 +0900 Prime / Composit Criterions
-------- Original Message No.30
--------
Subject: [theory-edge] The Schoolgirl's Homework Algorithm with No Blind Spot for
Primality Test
Date: Tue, 12 Apr 2005 11:05:19 -0700 (PDT)
From: Michiro Nasu <nasukun@yahoo.com>
To: theory-edge@yahoogroups.com
Hi Daniele and all!
We succeeded to make up an algorithm for primality test without
blind spot. I wrote a tiny program in UBASIC, and it is doing a good job on my machine with samples from 4
to 20 digits in 10-decimal system. Yet forget all of our terms? That's OK. All of what you
need is only the psi numbers.
Consider a natural number n on b-base decimal system. A psi
number y(b,n) is defined [for
numbers b and n mutually prime] as the smallest exponent
e such that be=1 mod n. We know that the Euler's
totient function f(n) satisfies bf(n)=1 mod n for any b mutually prime to n. Accordingly y(b,n)<=f(n), and it is certified that y(b,n) always divides f(n)
[18]. We use the following criterions to decide whether n is prime or composite.
| Prime Criterion: |
| A natural number n is prime iff there exists some base b such that y(b,n) = n-1. |
For example, let n=13, then n-1=12=2*2*3, y(2,13)=12 as 212=4096=1 mod 13. For other bases, y(3,13)=3, y(4,13)=6, y(5,13)=4, y(6,13)=12, y(7,13)=12, y(8,13)=4, y(9,13)=3, y(10,13)=6, y(11,13)=12, y(12,13)=2. As you see every psi numbers y are of a (possibly single) composite of factors of n-1. The ratio f(f(n))/f(n)=4/12=0.33333 is a good enough figure for us.
| Composite Criterion: |
| If n is an [odd] composite, then there exists some base b such that factors of the psi number y(b,n) forms a factor of n like the following manner. Suppose y and n have factors like y(b,n)=f1*f2*...*, and n=p1*p2*...*. Then for all factors pi of n, there exists some combination of factors taken from {f1, f2, ...} such that pi = fi1*fi2*...fik + 1. |
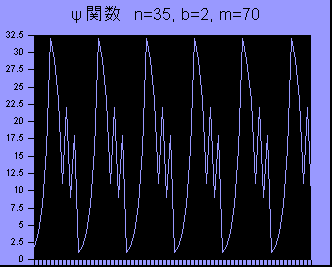
For example, let n=35 and b=2, then y(2,35)=12 as 212=4096=1
mod 35, and y(2,35) = 12 = 2*2*3 and n = 5*7 = (2*2+1)*(2*3+1).
Please look at the line again. I have not
encountered a paper citing this, but I believe that it is a fact.
As you notice our algorithm needs a perfect ability of factoring composites. In other
words, our algorithm must be a perfect factoring algorithm before being a complete
primality test. To perform the first criterion is not so hard provided we can factor the
number n-1, which is smaller than n and mostly even. It is sure that for every base b, y(b,n) must be a factor of n-1 and to say empirically we can find
such b as y(b,n)=n-1 with probability one in three.
 Only if we can have some set of candidates of a factor of
n, then to test them is easy, as just make a GCD of n and the factor candidate, and the
second criterion says that a psi number y(b,n) is a treasurer
of such possible factors. However here is a problem. In the first criterion, we could
infer a psi number from the factors of n-1. But in the second criterion, there is no such
material to use, and it is sure to seek a psi number from the bottom is quite a time
consuming.
Only if we can have some set of candidates of a factor of
n, then to test them is easy, as just make a GCD of n and the factor candidate, and the
second criterion says that a psi number y(b,n) is a treasurer
of such possible factors. However here is a problem. In the first criterion, we could
infer a psi number from the factors of n-1. But in the second criterion, there is no such
material to use, and it is sure to seek a psi number from the bottom is quite a time
consuming.
When I had almost abandoned the solution only by the mean of programming, I asked Toramasa
Ikeda, a skilled soft and/or hard-ware engineer of SONY corp to design a hard-circuit to
compute the Psi numbers, then he told me two things, "There
may be some abundance for b<<n, isn't it?", and "How does the differential of your formula go?".
With his advice I've drawn a graph (chart) of y=bx
mod n for fixed b and n. The figure above is an example of such a
function with n=35, b=2 and x in the range 1-70, which seems to be a cyclic function with
a cycle y(2,35)=12.
Please compare it with the terribly noisy figure of the
totient function y=f(x) and the psi function y=y(b,x) with fixed b at MSG#25. You
would agree that it is not impossible to get a residue=1
point in a feasible time in a way or another. Do you think/believe
that we can solve a 100 digits number problem on a small machine in a very near future?
Michiro
p.s. Again we are experiencing a difficulty to access the mail-server of our provider. So
I'll send this mail through a web-mail service. If you have an interest in the subject
please check our Repuit-Page at http://babalabo.blogdns.com/repunit/
.
-------- Original Message No.29 --------
Subject: [theory-edge] Re: Schoolgirl's Homework Conjecture] babalabo
Date: Sat Apr 2, 2005 8:51 am
From: Michiro Nasu nasukun@yahoo.com
To: Theory-Edge <theory-edge@yahoogroups.com>
Hi Daniele and all!
P5 is a proposal for a definitive primality test. I understand
that no known primality test is definitive, while P5 asserts that if y(b,n)=n-1,
then n is prime. I found a strong validity study for P5 at http://mathworld.wolfram.com/PrimitiveRoot.html.
Although its description is somewhat obscure, it is sure that the author meant that if n
and g are relatively prime and ord(g,n)=f(n), then g is a
primitive root of n. We know that the modulo order ord(g,n) is nothing but our y(b,n). So it reads that if y(b,n)=f(n), then b is a primitive root of n. We experimentally certified
that this is a firm fact through some observation.
As you see, if this is true, then P5 would follow straight. So the Burton
paper in 1989 is very crucial for us. Don't you have or have read the
paper? If you could access the paper, so wonderful, as our Congress Library in the capital
shut out we laymen from access foreign articles. Further if P5 is true, then Lehmer totient problem is about to be decided, although it might
still remain some uncertainty. BTW I wonder/fear if Lehmer Problem is Kelly-Ulam conjecture for Number Theory.
I wrote that P5 is not almighty since P4 states that every
repunit is an originator of itself. To show P4 is easy. For
example, 1000\111=9...1 => U=9, n=111, and nU/9=999/9=111. This means 111 originates
111. As you see it is simply impossible for the number 3=y(10,111)
of digits to be equal with the number 111 minus 1. However don't take it wrong.
It does not mean that for such a prime repunit, P5 does not hold. Let p be a prime repunit
p=R(b,y(b,p)) on some b-base, then there must be another base b*
such that y(b*,p)=f(p)=p-1.
The number of such base b* is f(f(p)),
which as we've just learned, is the number of primitive root of p. For example, for p=11, f(p)=10 and f(f(p))=4,
while
y(2,11)=10, y(3,11)=5, y(4,11)=5, y(5,11)=5, y(6,11)=10,
y(7,11)=10, y(8,11)=10, y(9,11)=5, y(10,11)=2, y(11,11)=0.
Thus b=2, 6, 7 and 8 are the primitive root of 11. E.g., for b=2,
{1,2,4,8,16,32,64,128,256,512,1024}=
{1,2,4,8,5,10,9,7,3,6,1} mod 11, and for b=6,
{1,6,36,216,1296,7776,46656,279936,1679616,10077696,60466176}
={1,6,3,7,9,10,5,8,4,2,1} mod 11, etc... Incidentally,
R(2,10)=1023=11*93=(210-1)/1,
R(6,10)=12093235=11*1099385=(610-1)/5,
R(7,10)=47079208=11*4279928=(710-1)/6,
R(8,10)=153391689=11*13944699=(810-1)/7.
As far as I observed, the ratio f(f(n))/f(n) is about 1/2-1/3. This is not so bad figure to seek a solution,
although P5 is of no use for composite numbers. In most cases f(f(n)) divides f(n), but it seems not
necessary. Consequently the first half of the statement P6 may not be well-formed yet, and
the second half is trivial. So I retract P6 at present. P7 may be worse, but I dont
mention it here, as we have to learn a bit more.
However I believe that this approach is not only able to give a definitive solution for
primality test but also very prospective for composites factoring. How is the distribution of primitivie root numbers b*. At
a glance it is not at all random. Don't you think that we can find a sweet spot to make a
decision without try and error.
Michiro
p.s. We are still involved in a great trouble. First I have to re-install the OS once
again as my mail client was broken accidently, and second as the result I lost all my
stock of in/out mails. Third now I cannot send nor receive mails through the mail server
of our provider. It was just unbelievable for me to have heard a voice mail recorded at
the telephone number of the office of our provider saying that they are in an unscheduled vacancy until April 7th. It means I cannot
expect the mail server to recover at least until Apr. 11. So I would send this post via a
web-mail service.
-------- Original Message No.28 --------
Subject: [theory-edge] Re: Schoolgirl's Homework Conjecture]
Date: Wed, 30 Mar 2005 13:41:16 +0900
From: babalabo <babalabo@aya.or.jp>
To: Theory-Edge <theory-edge@yahoogroups.com>
Hi Daniele and all!
Our Schoolgirl's Homework Conjecture was determined to be a
fact, i.e., for all non-radical numbers n, n originates a repunit number and divides
always by(b,n)-1 and the repunit R(b,y(b,n)). I'm so happy as I could solve the homework within a due
time. Yesterday I found a strong proof for [18], which states
that y(b,n) always divides the totient function f(n). Recall Lagrange's theorem.
| Lagrange's Group Theorem: |
| If G is a finite group and H is a subgroup of G, then the order of elements of H divides the order of G. |
Lagrange's theorem is provable by using the concept of left cosets of H in G. It is no hard to see that this theorem implies Fermat's little theorem, Euler's Totient theorem, and the proposition [18]. As you know for any prime p, Zp forms a finite field and Zp* is a cyclic group of order p-1. This corresponds to Fermat's theorem. While a modulo multiplication group Mn is defined as an abelian group of order f(n) which represents Euler's theorem.
We can derive an abelian group of order y(b,n) from our
formulation of by(b,n)=1 mod n, which gives a
subgroup of said modulo multiplication group of order f(n). Of
course the situation may be slightly different. For example we may think that n is a
variable, while they may regard it as a constant. Anyway I've returned back to Group
Theory starting at Number Theory. I wish Vlad would welcome back us. This recursion is of
no wonder as far as Group Theory is build up out of the base of natural numbers.
Let's go onward! The most important device in our invention is the u-length
function y(b,n). We now understand y(b,n) is equivalent what they call multiplicative
order, or simply modulo order denoted by ordna or On(a), i.e.,
ordna=y(a,n). Simultaneously our y(b,n)
is a sort of extension of the totient function f(n), so it is worthwhile
to determine to what extent y(n) is applicable instead of f(n), that is, to determine the working area of y(b,n).
The merit of y is that y value is
obtainable by just one time division and we need not to factor n as for the totient
function f(n). However I take it aside, and would like to go
into the depth. Now I propose the following propositions.
| P1 | If a prime p originates a repunit R(b,k), then k divides p-1. |
| P2 | If a number n originates a repunit R(b,k), then n divides R(b,k). |
| P3 | A repunit R(b,k) is factored into distinct repunits and primes. |
| P4 | A repunit number R(b,k) originates itself on any b-base. |
| P5 | If the u-length y(b,n)=n-1 for a number n, then n is prime. |
| P6 | If y(b,n) is a prime, then f(f(n))=0 mod y(b,n)-1 else R(b,y(b,n)) has repunit factors. This proposition is true even if n is radical. |
| P7 | (1) If n is fundamental, then y(b,n)=0.
(2) If n has just one non-radical prime factor, then y(b,n) is prime. (3) If n has more than one prime factors, then y(b,n) is composite. |
P1 is just a paraphrase of [18] and P2 of [9"]. Here I placed them parallel to
emphasize a Mebius like flavor between them. I think it relates to the hypothesis P3. P4
emphasizes a peculiarity of repunits numbers. A non-radical number originates a repunit
number and numbers which originate the same repunit are in an
equivalence relation, hence the relation partitions numbers. I want to know
what these equivalence classes are. P5, p6 and p7 are aimed to cut the edge and open the
can.
We know that if n is prime, then f=n-1. However the opposite is
still left open as it is a part of problem known as Lehmer's
Totient Problem, which asks if there exist
any composite numbers n such that f(n)|n-1. If such
a number exists, then it must be a Carmichael number because y(b,n)|f(n)|n-1, and then bn-1=1 mod n. No such number is known
so far. I dare to claim P6 to break through this stalemate, although P6 is not at all
almighty, for example this method cannot detect a prime repunit
since the y of a repunit number n could never be n-1 by P4.
IMHO the proposition if f(n)=n-1 then
n is prime must be proven first. However even if this proposition is proved,
it might not give us a definitively efficient algorithm for primality test because to gain
the totient function we need a factoring beforehand. Here is the difference as the
computation of y is so easy. BTW if y=n-1,
then of course f=n-1. Regarding P6, we know that y|f, so it is remarkable to hear y-1|ff from P6. These propositions were
obtained mainly through some observation of the repunit factoring table maintained
voluntarily.
Michiro
 p.s. I found out that Fermat was an amateur mathematician! Have you ever seen the statue at his
hometown Toulouse named "Fermat and his muse". When you look at this statue in the direct front of Fermat, he looks so serious and full of
dignity. However if you look at it a bit off the angle,
then he is intimately smiling at his muse.
p.s. I found out that Fermat was an amateur mathematician! Have you ever seen the statue at his
hometown Toulouse named "Fermat and his muse". When you look at this statue in the direct front of Fermat, he looks so serious and full of
dignity. However if you look at it a bit off the angle,
then he is intimately smiling at his muse.
Some examples for the account of the propositions:
P1 example: {xx,yy,..} is a set of repunit divisors {R(xx),R(yy),..}.
R6={2,3}*7*13, k=6, originator=7,13, while 7=k+1, 13=2k+1.
R29=3191*16763*43037*62003*77843839397, k=29, while
3191=110k+1, 16763=578k+1, 43037=1484k+1,
62003=2138k+1, 77843839397=2684270324k+1.
P2 example:
R6=111111/7=15873, 111111/13=8547
R29=1111..1/3191=3482015390508026045475121
=1111..1/16763=662835477606103389077797
=1111..1/43037=258175781562634735486003
=1111..1/62003=179202798430900296939037
=1111..1/77843839397=142735908161530363
P3 example:
R24={2,3,4,6,8,12}*99990001
R25={5}*21401*25601*182521213001
R26={2,13}*859*1058313049
P4: n=11, y(10,11)=2, (10^2-1)/9=11
n=111, y(10,111)=3, (10^3-1)/9=111
n=1111, y(10,1111)=4, (10^4-1)/9=1111
P5: in the range 2<=n<=600 for 2<=b<=16, no counterexample was found,
though the smallest Carmichael number is 561. the most curious is
that for b=a2=4,9,16..., I could detect no primes in this manner.
for some of smaller Carmichael numbers tested on 10-base:
n=561, f=320, ff=128, y=16
n=1105, f=768, ff=256, y=48
n=15841, f=12960, ff=3456, y=120
n=29341, f=25920, ff=6912, y= 60
P6 example:
R239=479*142847911*C228, y-1=238
n=479, f(479)=478,f(478)=238
n=142847911,
f(f(142847911))=36465408=238*153216
n=C228, f(f(C288))=...
R41=83*1231*538987*201763709900322803748657942361, y-1=40
n=83, f(f(83))=40
n=1231, f(f(1231))=320=40*8
n=538987, f(f(538987))= 149760=40*3744
n=201763709900322803748657942361, f(f(n))=...
-------- Original Message No.27 --------
Subject: Re: [theory-edge] Re: Schoolgirl's Homework Conjecture
Date: Sun, 27 Mar 2005 18:38:15 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Hi Daniele!
Thanks for your response.
| first I have to say that your messages are formatted in a nice manner, but as result they are not reported in the daily digests and I have some difficult reading them in parallel. |
Sorry, I've just received a yellow card from the referee.
| If I understand right you search {x,y,z} triples of nonnegative numbers such that for given n and b n*z+x=x*by |
Yes.
| In particular I understand that you defined y(b,n) the smaller y for which such a {x,y,z} pair exists. |
Exactly.
| It seems also that you need only that x < n, but this is on my opinion not too
interesting, as {x,0,0} is a valid triple for each x (also for all x < n), as in this
case n*z+x = n*0+x = x, and x*by = x*b0 = x |
If you act none, then x remains as it is.
| Note also that {0,y,0} is also a valid triple for each y. |
OK.
| Possibly you need a triple with a positive y and x,z not both zero. |
We need at least z>0.
| But in this case, if b is even and n=2, you find no valid triple, as 2*z+x=x*by |
OK.
| admits only triples with even x and thus x=z=0 or x >= 2 (possible triples are {0,y,0} and {2,y,by-1} for any y). Something similar also happens if b is a multiple of n, at least when n is prime. |
We have to exclude normal numbers (y=u-length=0). That is, factors of n must not be totally factors of b.
| On my opinion your definitions needs some adjustments. |
Thanks. I agree with you.
| But do not forget, that the necessity to add exceptions to a rule is often indication for a possible weakness of the rule itself. |
We call such numbers as above fundamental numbers.
For example, if b=10, then a number n=2p5q,p>=0,q>=0 is
fundamental on the base b.
BTW I've found out that basically all of what we had discovered is already known in Number
Theory, though some may be relatively recent. So apparently we were inventing a wheel. ^^;
As you see, if we could show that for non-radical numbers, r=1 is a solution, then it is
the only one solution as x=1 gives the minimum exponent y. They call the exponent y with residue x=1 the multiplicative order of b modulo n, or
alternatively the haupt exponent.
That is, by=1 mod n, and y gives the length y of the recursion unit of the reciprocal of n.
In general, if a<n and n are mutually prime, then there exists exactly one number
0<=m<=f(n)-1 such that bm=a mod n, called a general
multiplicative order, or alternatively discrete
logarithm. Seemingly this notion was out of our reach.
Michiro
-------- Original Message No.26 --------
Subject: Re: [theory-edge] Schoolgirl's Homework Conjecture
Date: Sat, 26 Mar 2005 12:47:32 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Hi Daniele and all!
I wrote,
| y(b,n)=0 for all numbers n of the kind called ultra-radical numbers all of which factors are a factor of the base b. For example, on 10-base numbers 2,4,5,8,16,.. have y(10,n)=0. |
Sorry. Although ultra-radical numbers are not yet
formally defined, in this context I misused the term against a notion in my brain. I meant
here fundamental numbers but not ultra-radical numbers. now let's give them a formal
definition.
Def: A number n on a b-base system is radical (with the
radix b) iff some factor of n is a factor of either b or b-1; otherwise n is non-radical.
As well an ultra-radical number is a number such that all of its factors
are a factor of either b or b-1, while a fundamental number is a number
such that all of its factors are a factor of the base b.
Note: Let F be the set of all fundamental numbers, U be the set of all
ultra-radical numbers, and R be the set of all radical numbers, then F < U < R. Let nR be the
number class ~R, where the proposition [9"] comes to that for all number n
\in nR, by(b,n)-1 is divisible by n. At the
URL below, you'll find a list of definitions appeared so far. http://babalabo.blogdns.com/repunit/index.shtml/#Definitions/
According to the above definition, the quote above must be rewritten like: "y(b,n)=0 for all numbers n of the kind called fundamental
numbers all of which factors are a factor of the base b. For example, on 10-base numbers
n=2,4,5,8,16,.. have y(10,n)=0."
It is almost sure that our recursion type "-" class
would be identified with the number class fundamental.
We noticed that the notion ultra-radical factor
would make the difference between the totient function f(n) and
the u-length function y(b,n). Proposition [18] says that y(b,n) always divides f(n). With some
observation, we certified a fact that a quotient f(n)/y(b,n) is always an ultra-radical
number. For example in 10-base, for n=1,2,...100,
f(n)/y(b,n)={
2,*,*,2,1,*,6,*,5,4,2,1,8,*,1,6,1,*,
2,5,1,8,*,2,6,2,1,8,2,*,10,1,4,12,12,1,4,*,
8,2,2,10,24,1,1,16,1,*,2,4,4,6,20,4,2,1,1,16,
1,2,6,*,8,10,2,2,2,4,2,24,9,12,40,2,10,4,6,*,
6,8,2,4,4,2,2,20,2,24,12,2,4,1,4,32,1,1,30,*},
where * is the case, divisor y(b,n)=0, i.e., the number n is fundamental. In the above list, all numbers appeared as a quotient f/y are ultra-radical, in other words, the number n is a product of only 2, 3 and 5. Especially on 2-base, it is certified that every quotient f/y is a form of 2k. I think that this fact would become some help for us preparing for the proof of proposition [18]. So I raise it here as lemma [19].
| [19] | For any b-base decimal system, for any number n with y(b,n)>0, the quotient f(n)/y(b,n) is an ultra-radical number on the base b, where f(n) is the Euler's totient function and y(b,n) is the u-length function of n. |
Michiro
-------- Original Message No.25 --------
Subject: Re: [theory-edge] Schoolgirl's Homework Conjecture
Date: Fri, 25 Mar 2005 16:42:03 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Hi Daniele and all!
The totient function f(n), also called Euler's
totient function, is defined as the number of integers <=n that are mutually prime to
n, while our u-length function y(b,n) is defined as the minimum
number of recurrent digits of the inverse 1/n of the number n on b-base decimal system.
Proposition [18] states that for any number n>2, y(b,n)>0
divides f(n) on any b-base system. I provided a
drawing of the functions in the range 1<n<=100 to see how they look like. Apparently
[they are] not at all a simple function, but something like a noisy oscillator output.
However you would notice sooner or later that there exists some harmonics/multiplicity
comparable to the codes of music. Please listen to the sound of numbers for a while...
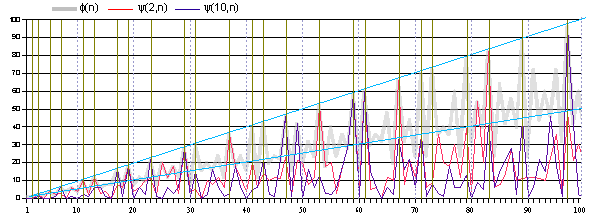
It is easy to see that for every prime p, f(p)=p-1.
Consequently every prime (on the brown vertical line) is at the peaks of function f(n). In this sense totient function is preferable to a
u-length function for the purpose to distinguish primes. However to calculate a value f(n), you need a total factoring of the number, while a value y(b,n) is computable just by a simple division of at most n times.
y(b,n)=0 for all numbers n of the kind called ultra-radical
fundamental numbers all of which factors are a factor of the
base b. For example, on 10-base, numbers n= 2,4,5,8,16,.. have y(10,n)=0.
Michiro
Rem: The quotients f(n)/y(10,n)
for n=1,2,3,...100 are in a form n:f/y, {
3:2, 6:2, 7:1, 9:6, 11:5, 12:4, 13:2, 14:1, 15:8, 17:1, 18:6, 19:1,
21:2, 22:5, 23:1, 24:8, 26:2, 27:6, 28:2, 29:1, 30:8,
31:2, 33:10, 34:1, 35:4, 36:12, 37:12, 38:1, 39:4,
41:8, 42:2, 43:2, 44:10, 45:24, 46:1, 47:1, 48:16, 49:1,
51:2, 52:4, 53:4, 54:6, 55:20, 56:4, 57:2, 58:1, 59:1, 60:16,
61:1, 62:2, 63:6, 65:8, 66:10, 67:2, 68:2, 69:2, 70:4,
71:2, 72:24, 73:9, 74:12, 75:40, 76:2, 77:10, 78:4, 79:6,
81:6, 82:8, 83:2, 84:4, 85:4, 86:2, 87:2, 88:20, 89:2, 90:24,
91:12, 92:2, 93:4, 94:1, 95:4, 96:32, 97:1, 98:1, 99:30},
while f/y=1 for {14, 19,
23, 29, 34, 38, 46, 47, 49, 58, 59, 61, 94, 97, 98},
and primes f/y=\=1 are
{3, 11, 13, 31, 37, 41, 43, 53, 67, 71, 79, 83, 83}.
No remarkable fact is observed between a number n to be a prime and the value f/y of n.
-------- Original Message No.24 --------
Subject: [theory-edge] Schoolgirl's Homework Conjecture
Date: Thu, 24 Mar 2005 12:11:48 +0900
From: babalabo <babalabo@aya.or.jp>
To: Theory-Edge <theory-edge@yahoogroups.com>
Hi Daniele and all!
I've still stuck at proposition [9]. Now I understand that it is no
easy at all but a bit hard problem. However my confidence for the conjecture is very
strong. My estimation of the probability for the conjecture to be true is all about
0.9999999999. So I can bet you whole my life for that.
Fermat's little theorem states that for any prime p, bp-1-1
is divisible by p on any b-base. This theorem is the fundamental of Number Theory. Euler's totient theorem extends it to general number n mutually
prime to b stating that bf(n)-1 is
divisible by n, where f(n) is the Euler's totient function. Our conjecture [9] is an extension of
Euler's theorem along this line. The final form of [9] comes like this.
| [9"] | Schoolgirl's Homework Conjecture: Let y(b,n) be the minimum number of recurrent digits in b-base decimal representation of the inverse 1/n of a number n. Then for all natural numbers n>1 mutually prime to b and b-1, by(b,n)-1 is divisible by n, as well the repunit number R(b,y(b,n)) is a multiple of n. |
Number Theory is the most matured domain in mathematics and has investigated
intensively for a long time since the beginning of human history. So I feel a hesitation
if I claim that this is the first discovery by us alone. However I believe that at least
our approach is somehow new and worthwhile to pursue. Please inform me if you know
anything about this.
As you know in decimal number expression, every rational number has either a fixed length
of digits or an infinite recursion. Our investigation is focused to the relation between n
and the inverse 1/n. It is easy to see that the length y(b,n)
of a recursion unit of 1/n is always smaller than n.
Suppose that we are going to divide 1 by n>1. Since 1 is smaller than n we first
multiply 1 by bm so as to 1*bm >n. Then we divide the dividend
1*bm by n and obtain Q=1*bm\n...R, and would continue this process
until we find out a remainder R that occurred previously. If a remainder R occurs twice in
a dividing process, then R...R steps must be repeated endlessly. However from R<n, it
is concluded that the division steps, i.e., the length of a recursion unit shall never be
more than n. Thus y(b,n)<n.
Def: Given natural number n>1, there exist nonnegative integers x,y
and z such that z=x*by \n...x, that reads n divides x*by, the
quotient z, and the remainder x<n, in other words, n*z+x=x*by. Obviously a
set of {x,y,z} exists infinitely. So we define u-length function y(b,n) as the minimum such number y, as well recursion
unit U(b,n) as the minimum such number z. Accordingly we have n*U(b,n)=r*(by(b,n) -1), where r is the first dividend
that eventually appears as the remainder.
We may call this equation the recursion equation but
not call it recursion formula because we know that a set of
{x,y,z} satisfying the equation does not necessarily appear in an actual
dividend-remainder sequence. Indeed the equation holds for any x against given
n. For example, given n=21, you easily find out the remainder sequence
{1,10,16,13,4,19,1,..}, while u-length function y(10,21)=6,
U(10,21)=47619 and r=1. However if you take U=47619*x and r=x, then the equation holds for
any x. I need your help!
To fortify the continuity between our conjecture and Euler's theorem, I would like to
raise one more proposition [18]. A strange flavor of this proposition comes from the fact
that function f(n) is
base-independent, while y(b,n) depends on base b.
The truth probability of this conjecture is also about 0.999999... Please find a
counterexample or show the proof.
| [18] | For any natural number n>2 on b-base decimal system, the value of u-length function y(b,n)>0 always divides the value of Euler's totient function f(n), i.e., gcd(f(n),y(b,n)) = y(b,n). |
Michiro
mailto:babalabo@aya.or.jp
http://babalabo.blogdns.com/repunit/
p.s. For your convenience, here is a VB code for calculating u-length function y and totient function f.
PFactor(n) is a function which returns the smallest prime factor of n.
Function Psi(num As Long, b As Long) As Long Dim RT() As Long Dim x As Long Dim q As Long Dim r As Long Dim n As Long ReDim RT(num + 1) n = num x = 1 RT(0) = x For i = 1 To n x = x * b If x >= n Then q = x \ n r = x Mod n If r = 0 Then Psi = 0 Exit Function End If For j = 0 To i - 1 If r = RT(j) Then Psi = i - j Exit Function End If Next j x = r Else q = 0 r = x End If RT(i) = r Next i End Function Function Phi(num As Long) As Long Dim p As Long Dim result As Long Dim n As Long n = num result = n While n > 1 p = PFactor(n) While n / p = Int(n / p) n = n / p Wend result = result - result / p Wend Phi = result End Function
Rem: The function Phi above is written by Takeuchi, Niigata University, http://www2.cc.niigata-u.ac.jp/~takeuchi/tbasic/ . His Tiny Basic is available at http://www2.cc.niigata-u.ac.jp/~takeuchi/tbasic/English/index.html .
If you have a question why proposition [9"] is "Schoolgirl's Homework Conjecture", check my first post at http://groups.yahoo.com/group/theory-edge/message/10956.
-------- Original Message No.23 --------
Subject: [theory-edge] Re: Repunits as multiple (was Recurrent Numbers)]]
Date: Sun, 20 Mar 2005 10:47:59 +0900
From: babalabo <babalabo@aya.or.jp>
To: Theory-Edge <theory-edge@yahoogroups.com>
Hi Daniele and all!
I'm very glad to come up to the point to respond your post now.
| I can now state following theorem Given a number a and a number n relatively prime to b, then for all k ak*f(n)-1 is a multiple of n where f(k) is the Euler totient function. |
OK. Let me paraphrase it.
[9'] In b-base decimal system, for all non-radical numbers n, there
exists a repunit number R(b,f(n)) originated from the
number n, where f is the Euler totient function.
| This is just a reformulation of the Euler Totient Theorem |
That's right. This Euler Totient Theorem is still a wonder for me, really a product of supremacy genius as well as Euler's Formula. Euler (1707-1783) wrote 75 volumes of books and papers, a half of which were written for his last seventeen years, when he was completely blind! http://leonhard-euler.biography.ms/
| http://mathworld.wolfram.com/EulersTotientTheorem.html |
Thanks.
| It follows directly that for each odd n not multiple of 5 there exists an infinite number of repunits multiple of n. |
Now I agree with you as we are confirmed by [17].
| Note that for a prime p, f(pk) = (p-1)pk-1
and thus my previous conjecture follows also directly from above theorem. |
I think we've cleared almost questions. In my next mail I will try cleansing house a
bit and would seek the direction from now on.
Michiro
Rem: In above description Daniele adapts k*f(n) as the power of the base while I only use f(n). This difference is due to the difference of motivation. DGD intends to expand to the extent while my intention is to restrict within the repunits originated by the number n and clarify the critical border.
The number of numbers under n is n-1 and for a prime every number
under p is mutually prime, hence f(p)=p-1, while pk
is still prime for any other numbers and f augments by
pk-1.
-------- Original Message No.22 --------
Subject: Re: [theory-edge] Re: Repunits as multiple (was Recurrent
Numbers)
Date: Sat, 19 Mar 2005 01:49:29 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Hi Daniele and all!
Now I've got a proof of [D3]! at first I will prove a few lemmas. But beforehand I'd like
to amend the definition of non-radicals.
Def: A number n is non-radical in b-base decimal system if n is mutually prime to both b and b-1; otherwise n is radical.
Hereafter let R(b,u) denote a b-base repunit number of u-length u.
| [15] | For any b-base decimal system and natural numbers m and n, if n is divisible by m, then R(b,n) is divisible by R(b,m). |
Proof of [15]: By the premise n=m*q, and by the definition of repunit number, R(b,n) is a m*q copies of digit 1. We partitioned them into q segments of repunit R(b,m) of u-length m.
| R(b,n)=R(b,m*q) | = S[i=0 to n-1] bi |
| = S[i=0 to q-1] ((bm)i
* S[j=0 to m-1] bj = S[i=0 to q-1] (bm)i * R(b,m) = R(bm, q)*R(b,m). |
Thus if m divides n then R(b,m) divides R(b,n). QED.
Note: [15] is essentially equivalent to [D1], so to say
another proof of [D1]. As we did not use prime condition, this proposition holds for any
composite. From above we can derive two expressions of a composite repunit, i.e., R(b,n)
has two divisors on b-base, either R(b,m) or R(b,q), and for each we have a different
expression,
R(b,n) = R(b,m*q) = R(b,m)*R(bm,q) = R(bq,m)*R(b,q).
Now we understand that regarding a repunit R(b,n) as a unary number of string length n,
multiplication/division of repunits obeys the rule of ordinary integer
multiplication/division assuming that any division do not leave a remainder. It is very
important to recognize that these operations are base-independent. That is, the u-length
of a repunit number is considered to be some kind of invariant.
| [16] | For any b-base decimal system and natural numbers m and n, if n is a square of m, i.e., n=m2 then R(b,n) is divided by R(b,m). |
Proof of [16]: Similar to the proof of [15],
| R(b,n) | = S[i=0 to n-1] bi |
| = S[i=0 to m-1] (bm)i
* S[j=0 to m-1] bj = S[i=0 to m-1] (bm)i * R(b,m) = R(bm,m) * R(b,m) |
Thus R(b,m) divides R(b,n), and the quotient Q=R(b,n)/R(b,m)=R(bm,m).
Note: This is a mere corollary of [15]. I just wanted to see how the quotient would look
like, and we've got R(b,m2) = R(b,m)*R(bm,m).
This means that a repunit number R(b,m2) of a square m2 is factored
asymmetrically into two repunits R(b,m) and R(bm,m) with the same u-length m.
Now let's try the next proposition.
Proposition: If a prime p is non-radical in both bases of b and bp-1,
then repunit R(b,(p-1)2) is divisible by p2.
Proof: From the above reasoning we know that a b-base repunit R(b,(p-1)2)
is to be factored into R(b,p-1) and R(bp-1,p-1). By the premise p is prime and
mutually prime to both b and bp-1 base. hence by [10'],
p divides both R(b,p-1) and R(bp-1,p-1). qed.
However this proof includes a fatal flaw. Because for the base bp-1 of the
second repunit, p always divides bp-1-1. This is what Fermat
tells us. In other words, no prime p is non-radical simultaneously on the bases both b and
bp-1. Here comes the proposition [D3]. Now you understand
why the Daniele's formula is asymmetric.
| [17] | For a non-radical prime p on b-base, repunit R(b,(p-1)*p) is divisible by p2. |
As I wrote at the note for [15], a factoring of a repunit has two varying expressions. In this case, we can divide the repunit R(b,(p-1)*p) either/both by R(b,p-1) or/and R(b,p) like the follows.
| R(b,(p-1)*p) | = R(b,p-1)*R(bp-1,p) | (1) |
| = R(b,p)*R(bp,p-1) | (2) |
Let's take the first one. by Fermat's little theorem, R(b,p-1) is divisible by p and by [15], R(b,(p-1)*p) is a multiple of R(b,p-1). All of what we need is to show that the quotient R(b,(p-1)*p) / R(b,p-1) = R(bp-1,p) is divisible again by p. Let's see it. It may be helpful to recall R(b,u)=(bu-1)/(b-1)=S[i=0 to u-1] bi.
| R(bp-1,p) | = S[i=0 to p-1] (bp-1)i |
| = S[i=0 to p-1] ((bp-1)i
-1 + 1) = S[i=0 to p-1] ((bp-1)i - 1) + p = S[i=1 to p-1] (b-1)*R(bp-1, i) + p = (b-1)*S[i=1 to p-1] R(bp-1, i) + p |
The last term above is p and of course a multiple of p; the first term S[i=1 to p-1] R(bp-1,i) would look like in bp-1-base,
111111111...1
+1111111....1
+111.......1
:
:
+11
+1
-------------
123.........p-1
Each i-th digit of the sum comes to be (p-i)*(bp-1)i. Further,
S[i=1 to p-1](p-i)*(bp-1)i
= p*S[i=1 to p-1](bp-1)i
- S[i=1 to p-1]i*(bp-1)i
The first term of the sum fell into a multiple of p. For the second, we can use the
technique applied to show that a multiple of 3
has a digit sum divisible by 3.
| S[i=1 to p-1] i * (bp-1)i | |
| = S[i=1 to p-1] (i *
(bp-1)i - 1) + i) = S[i=1 to p-1] i * ((bi)p-1 - 1) + S[i=1 to p-1] i |
|
By Fermat's ((bi)p-1-1) in the first term is a multiple of p. For
the second term, S[i=1 to p-1]i = (p-1)*p/2. thus
R(b,(p-1)*p) is divisible by p, and then R(b,(p-1)*p) is a multiple of p2. QED.
Note: It is easy to extend this result to general formula in [D3]. Now we clearly
understood that for all number n there exist infinite number of
repunits multiple of n provided you dont care which is the base. Even if you are
sensitive to the base b, it is sure that there exist infinite number of repunits that is
multiple to n only if n is non-radical on b. Supposedly we finally settled our proposition [9] problem, and here I declare that [9]
is established as a theorem after that [D3] is able to be proven with no
reservation.
Michiro
p.s. Klaus: Thanks for your help. Just the best timing for you to send me a small tool
written in Smalltalk on Squeak
environment. If I haven't it, I may be still stuck around the point. \(^^)/
Readers: A much more readable and well formed page for this thread is here http://babalabo.blogdns.com/repunit. It is
a single web page containing tables of definitions, propositions and questions. Updated
daily base along the progress of the discussion.
-------- Original Message No.21 --------
Subject: Re: [theory-edge] Re: Repunits as multiple (was Recurrent
Numbers)
Date: Wed, 16 Mar 2005 22:58:00 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Hi Daniele!
Thanks for your answer.
| just a short proof to the last question. 111 is obviously multiple of 3. |
Yes.
| 1001001 is also a multiple or 3 (digits sums up to a multiple of 3). |
Very good. I learned this when I was an elementary schoolboy from a famous book (in
Japanese) by Centro Yano. Let's recall it.
Proposition: Given b-base decimal number system, and let f
be a factor of b-1. Then a number n is divisible by f
iff the sum of each digits of n is divisible by f.
Proof: Suppose b-base representation of n = S[i=0 to m]ai*bi. Rewrite the right side as
n = S[i=1 to m]ai*(bi-1)+S[i=0 to m]ai.
As you know (bk-1) is always divisible by (b-1), hence by premise divisible by f. Consequently n mod f = S[i=0 to m]ai mod f. QED.
| 111*1001001 = 111111111 and is multiple of 32. 1000000001000000001 is again multiple of 3 and multiplying it with 111111111 you get a number with 27 ones that is surely multiple of 33. you can continue at libitum. |
OK. Now we understand that at least for some b-base system and a factor f of b-1, [D3] holds. That is, for all primes p, there exists
some b>p such that p divides b-1 and satisfies the following,
(b(p-1)*p^k)-1)/(b-1) = 0 mod pk+1.
Can't you generalize this? Perhaps all of what you need to prove is that for any b-base
system a number n of form 100...0100....0100...1 is divisible by n, where the recursion
part 100...0 is of length n and the number of the recurrence is also n. It seems to me no
hard...
m.n.
-------- Original Message No.20 --------
Subject: [theory-edge] Re: Fwd: Re: Repunits as multiple (was
Recurrent Numbers)
Date: Wed, 16 Mar 2005 12:27:43 +0900
From: babalabo <babalabo@aya.or.jp>
To: Theory-Edge <theory-edge@yahoogroups.com>
Hi Daniele!
| I think I have found that for a prime number p, the repunit (10(p-1)*p^k-1)/9 is multiple of pk+1. |
I think affirm that this assertion is likely to be true. Perhaps you
inferred this from your observation w.r.t. 3k
which I asked you a hint. A repunit number has a form 111...11 and this form is very
resemble to what they call unary representation of numbers in
complexity theory. Usually a unary number n takes a form of string "000...00" of
its length n. So it is quite natural to regard our repunit number as a kind of unary
numbers and expect an arithmetic relation on it.
In general a repunit number Rn is defined as Rn=(bn-1)/(b-1).
The power n represents the length of the repunit. So we will call it a repunit
length or shortly u-length. For the above formula, u-length
u=(p-1)*pk. Obviously/surprisingly a repunit length is base-independent.
So the above assertion must hold for any base. Readers may think that it is almost
unlikely, but if you understand what's Fermat's theorem all
about, then you may accept it. For example Fermat says that for all primes [with some
exception], for any base a repunit of length p-1 is divisible by p. Let's make a sampling
test for p=11 case.
R2(10)=1111111111(2-base)=1023, 1023/11=93
R8(10)=1111111111(8-base)=153391689, 153391689/11=13944699
R10(10)=1111111111(10-base)=1111111111, 1111111111/11=101010101
R16(10)=1111111111=(16-base)=73300775185, 73300775185/11=6663706835
As you see above, regardless the base of the system,
repunit numbers of the same length are divisible by the same prime 11, where Rb(u)
denotes a b-base repunit number of length u. That is,
Fermat's theorem is a very strong support for Daniele's formula, conversely that
is an ultimately wide expansion of the Fermat's theorem. Now let's the formula identify [D3].
I expect the assertion [D3] to be proven not in an algebraic direction, rather by an
arithmetic/operational way.
| For the cases cited in the previous mail I found out that (10294-1) is multiple of 73 and (10272-1) is multiple of 172. |
294=2*3*72 and 272=24*17. 7 is a prime which originates R6. Hence 294 is accountable by [D3]. that is, u(p)=6 and u(p3)=6*72. Also the latter comes to like: 17 has a repunit R16, hence u(p)=16 and u(p2)=16*171.
| Proving this would imply your theorem 9, i.e. that for each odd number q not multiple of 5 there are infinite many repunits multiple of q. |
Now let's define a name for a prime/a factor which is mutually prime to the base. We
will call such a prime non-radical prime or non-radical factor.
On the other hand, such numbers as 2p*5q are called radical
numbers. It is because a base is also called a radix. We think
that the proposition [9] is bi-directionally true. Hence we
have to prove,
(1) A repunit number has non-radical factors, but no radical factors.
(2) A non-radical number originates a repunit.
(2.1) A non-radical number is a factor of some repunit.
Of course (2) implies (2.1) and perhaps (1) is provable easily. In fact we already proved Lemma [6] which is 10-base version of (1). I think that it is
very critical for [D3] to cover (2.1) because IMHO [D2] barely holds for all the different
primes and even with the theorem [D3], it still remains a slight question for the strength
of the statement.
Fermat's theorem has two formulas w.r.t. repunit numbers. One is the form of bn-1
and the other is the form of bp-1-1. The former corresponds to our originator things. So if we can relax somewhere of the statements,
we may get the whole figure at once. You almost blew up the mist surrounding us, and now
we are crossing the [a tight] bridge over the river.
Michiro
-------- Original Message No.19 --------
Subject: [theory-edge] Re: Repunits as multiple (was Recurrent
Numbers)
Date: Tue, 15 Mar 2005 12:14:01 +0900
From: babalabo <babalabo@aya.or.jp>
To: Theory-Edge <theory-edge@yahoogroups.com>
Hi Daniele!
Sorry for my late response.
| Recalling some simple notion from algebra, in every polynomial field, xk-1 is a multiple of x-1. Moreover if k is composite, say of the form p*q*r..., then xk-1 is a multiple of all xp-1, xq-1, xr-1,... |
Yes, you are right if I take it straight.
[D1]: Verification,
(1) k=p*q*r... => xk-1 = (xp-1)*A = (xq-1)*B = (xr-1)*C...
(2) Rk is a multiple of each Rp, Rq, Rr....
(3) Further, if Rp, Rq, Rr are mutually prime, then Rk
is a multiple of Rp*Rq*Rr...
Note: Here p, q, r.. need not to be a prime.
| If p is a prime different from 2 and 10, then as you said by Fermat, 10p-1-1 is a multiple of p. |
Exactly, assuming you meant "2 and 5".
Fermat's theorem:
10p-1-1=p*X => for all primes p excluding 2 and
5, there exists a repunit Rp-1 divisible by p.
| Combining previous notions, we get easy that for each primes p,q,r,... > 5, there are infinite repunits multiple of p,q,r, ... and each combination of them (p*q, p*r, p*q*r, ...). |
[D2]: Verification (modified),
(1) By Fermat's: a repunit Rp'=Rp-1 is divisible by the prime p,
where p'=p-1.
(2) Let k be a number such as k=p'*q'*r'*...=(p-1)(q-1)(r-1)....
(3) Then by [D1] there exists a repunit Rk such that Rk is a
multiple of each Rp', Rq', Rr'....
(4) Therefore by (1) Rk is a multiple of each p, q, r...
(5) Assume that p, q, r... are distinctive primes, then Rk is a multiple of
p*q*r...
Note: At point (5) we assumed that every
primes p, q, r,.. are different. While k, p', q',
r',.. are always even and of course not prime.
| > for example, 1010-1 is a multiple of 11, and also 1020-1, 1030-1, ... |
1020-1=(1010-1)*X=R10*10000000001
1030-1=(1010-1)*Y=R10*100000000010000000001
1040-1=(1010-1)*Z=R10*1000000000100000000010000000001
Note: 1020-1 cannot be divided by (1010-1)*(102-1). In
this case 20=10*2=(11-1)*(3-1), hence p=11, q=3, and 1020-1 is divisible by
11*3=33. 1030-1 cannot be divided by (1010-1)*(103-1). In
this case 30=10*3=(11-1)*(4-1), hence p=11, q=4, but 1030-1 is not divisible by
11*4=44 as 4 is a power of 2 and not a prime.
30=1*30=2*15=3*10=2*3*5 and 1030-1 has at least factors 3, 11 and 31 while 4,
6, and 16 are discarded. Take care that the repunit Rk is
divisible by p*q*r*... even if Rk is not divisible by the product Rp,*Rq,*Rr'...
provided the primes p, q, r... are all the different.
| This covers your theorems 8 and 10, and a part of theorem 9. |
Yes, Fermat's implies [8'] and [10]. [9] claims that for all numbers mutually prime with 2 and 5 are originators of some repunits. [D2] asserts that for all such numbers n without power factors, there exists a repunit number Rk divisible by n. But this does not assure that n originates Rk.
| It is not clear if for all prime p there are repunits multiple of all powers of p. |
Your concern is reasonable as a power pk of a prime p is considered to be the kind of composites. Conversely, is it always possible to make a repunit which is consist of arbitrary distinct primes?, that is, a repunit which has no power factors?
for example 1042-1 is a multiple of 72, 1022-1 is a multiple of 112 and 1078-1 a multiple of 132. Curiously 42=6*7 and 78=6*13. 1066-1 is also a multiple of 112, but this terminates here, as 17*6=102 and 10102-1 is not even multiple of 17. For the moment I have not found any repunits multiple of 172 and any one multiple of 73.
Note: 7 and 13 originate R6, R2 originates from 11, and R16
from 17, while R42 is divisible by R6=O(7,13), R22 by R2=O(11),
R78 by R6=O(13), as well as R66 by R2=O(11)
where O(n) denotes a repunit originated from n. Here is a recursion
table 2<=n<=50.
Q1: 10102-1=1017*6-1 is not a multiple of 17. Why?
A1: 10102-1 is a multiple of each term 1017-1 and
106-1. but 1017-1 is not a multiple of 17. Fermat says that 1016-1
is a multiple of 17, but 1017-1 is probably not.
If you like a repunit of a multiple of 17, rather take 1016*6-1=1096-1.
Q2: It seems that there does not exist a repunit of a multiple of 172.
A2: 17 divides R16=(1016-1)/9. hence 1016*16-1=10256-1
might be divisible by 172. Have you tried it?
Q3: It seems that there does not exist a repunit of a multiple of 73.
A3: 106-1 is divisible by 7. hence 106*6*6-1=10108-1
might be divisible by 73. Have you tried it?
3 is a special case (as 9 is a multiple of 3), but it should be easy to show that (103^k-1)/9 is multiple of 3k, i.e. 111 is multiple of 3, 111111111 is multiple of 9, 11...11 (27 one) is multiple of 27 and so on.
I suppose that you probably use some kind of mathematical induction to raise this
proposition. But I can't solve it just now. If you like give me a hint or a solution.
M.N.
-------- Original Message No.18 --------
Subject: Re: [theory-edge] Re: Recurrent Number
Date: Mon, 14 Mar 2005 07:36:45 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Hi Richard and all!
You wrote,
| mind for the job is not a repunit. If you can back up a bit, simplify, define the terms you are using, give some concrete, finite examples such that I may more easily understand what you are talking about, then I would be of help to the extent of my ability. At present, unfortunately, your conundrums pale in comparison to my own, but I'm certain that is due only to my miscomprehension. I am |
Now I opened a web-page which I call Repunit-Page gathering my posts to this list. It is
just a collection of my posts and not a complete summary as it is too early for that, but
it is edited somehow to help your comprehension. I built it rather for myself as my
mail-client was broken by an accident and everything fell into a mess. It took me a time,
but I found some new facts overlooked in past through the task. Anyway please check the
link below. I believe you enjoy it.
http://babalabo.blogdns.com/repunit/
Michiro
p.s. I have to write small tool programs again for tests, especially to answer Daniele's
proposal. Klaus recommended me to use Smalltalk. I was considering to use an interpreter
language and Squeak is a development environment with Smalltalk interpreter. So I
challenged it, but found that it is no easy to learn rapidly. Perhaps I'll write down a
multi-precision arithmetic in C++ by myself as it is no hard at all. The merit is it
allows me to define custom operators.
-------- Original Message No.17 --------
Subject: Re: [theory-edge] Re: Repunits as multiple (was Recurrent
Numbers)
Date: Fri, 11 Mar 2005 06:10:34 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Hi!
| as a mathematical visa commercial might go.. "an interesting thm, $x. an interesting proof of an thm, $y. a picture of the theorem.. $x^y!!" |
A good saying! it may seem that we are just faithfully tracing an old passage
established in 18th century. But you would see sooner or later the difference, although
it's very subtle and somewhat skewed. I hope this ends in a happy hill climbing...
m.n.
-------- Original Message No.16 --------
Subject: Re: [theory-edge] Re: Repunits as multiple (was Recurrent
Numbers)
Date: Thu, 10 Mar 2005 04:47:42 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Daniele,
Read your proposal, just great! Really a splendid result! What a happy day! Indeed I've
not expected this. Do you know that today is my birthday? Thanks so much for your big gift
for my day.
But I'll bite it later since as I wrote in my mail to you, currently my teeth is being
carious (hard attacked by a virus sent from a person who called him/herself D. Pehoushek)
and far from comfortable. My small handcrafted tools were all lost in the mess. I'm
considering to absolutely re-install the OS into my computer, and maybe it would take at
least a day full. Please give me a time.
Michiro
p.s. I haven't yet digest your assertion at all, but I wonder if the Euler totient
function may talk anything around the existence of the pseudoprimes or not.
| Hi Michiro, I can now state following theorem Given a number a and a number n relatively prime to b, then for all k a^(k*\phi(n))-1 is a multiple of n where \phi(k) is the Euler totient function. This is just a reformulation of the Euler Totient Theorem http://mathworld.wolfram.com/EulersTotientTheorem.html It follows directly that for each odd n not multiple of 5 there exists an infinite number of repunits multiple of n. Note that for a prime p, \phi(p^k) = (p-1)p^(k-1) and thus my previous conjecture follows also directly from above theorem. Daniele --- In theory-edge@yahoogroups.com, "dgdegiorgi" <degiorgi@h...> wrote:
|
-------- Original Message No.15 --------
Subject: Re: [theory-edge] Repunits as multiple (was Recurrent
Numbers)
Date: Thu, 10 Mar 2005 03:09:22 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
I'm sorry. Now I understand what you meant.
I wrote,
| If I read above correctly, it says that xk-1 takes a form of (xp-1)(xq-1)(xr-1).... But I cannot get it. E.g. suppose k=6=2*3, then it becomes (a6-1)=(a-1)(a+1)(a2-a+1)(a2+1+1). Where I was wrong? |
Assign b=a3, then we have a6-1=(b2-1)=(b-1)(b+1)=(a3-1)(a3+1)
as well as a6-1=(a2-1)(a4+a2+1). Please laugh
my ignorance. m.n.
-------- Original Message No.14 --------
Subject: Re: [theory-edge] Repunits as multiple (was Recurrent
Numbers)
Date: Thu, 10 Mar 2005 02:48:46 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Hi Daniele!
Thanks for you response. However I stumbled at the beginning.
| Recalling some simple notion from algebra, in every polynomial field, xk-1 is a multiple of x-1. Moreover if k is composite, say of the form p*q*r..., then xk-1 is a multiple of all xp-1, xq-1, xr-1,... |
If I read above correctly, it says that xk-1 takes a form of (xp-1)(xq-1)(xr-1)....
But I cannot get it. E.g. suppose k=6=2*3, then it becomes (a6-1)=(a-1)(a+1)(a2-a+1)(a2+1+1).
Where I was wrong?
michiro
-------- Original Message No.13 --------
Subject: Re: [theory-edge] Re: Recurrent Number
Date: Wed, 09 Mar 2005 08:32:59 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Hi Richard and all!
In my previous mail I proved theorem [8']. It may be small but a very important step.
While we noticed the difference between our formation and others. Although I haven't yet
got the proof of the proposition [9], I'm sure that it is a fact. Proposition [9] says
that every number n which has neither 2 nor 5 has a repunit number Rk. If the
existence of a repunit is a necessary condition for a number to be a prime, we can detect
almost nothing by the repunit
criterion. For example 21 is a composite but has a repunit number 111 with recursion unit
037. Anyway go onward groping the darkness. Now we need a name for a number which
generates a repunit number Rk.
Def: Suppose a number n and its recursion unit U(n). If
nU(n)/9 forms a repunit number Rk, then we say that n is an originator
of Rk.
In general originator n of a repunit number Rk is a factor of Rk,
but it is not always. For example pseudoprimes 33 is an
originator of R2=11 but of course 33 does not divide 11. Similarly a factor n
of a repunit Rk is not necessarily an originator of Rk. For example
33 is a factor of R6 but not an originator of R6.
An arbitrary number n is an originator of at most one repunit, while a repunit number Rk
possibly has multiple originators. E.g. Repunit number 111 has at least 4 originators 7,
13, 21 and 39. We already know that there exist at least 2 repunits which contains a prime
p as its factor, while if a number n is an originator of a repunit Rk, then Rk
is the smallest repunit that contains n as a factor.
A pseudoprime of base-10 first appears at n=33, while in our method both 21 and 27 already
have repunit numbers. In this point of view our method seems pale before any ordinary
method. But it isn't. We don't yet consider other conditions than repunit numbers. Recall Fermat's theorem stating that k divides n-1. let's check it.
OK. Just it works. If n is a prime then it is always n-1=a*k. Consequently we can say that our method is no weaker than Fermat's primality test. Now let's go into the recursion unit itself.
You may notice the peculiarity of 3 and 33 of which recursion unit is not divisible by 9. This means that n has at least one factor 3. Thus we detect pseudoprime 33 using the knowledge of recurrency in decimals. However our reasoning is still weak for general cases. We need a bit much stronger munitions.
In the table above, 3,9,27 and 33 fails to divide its repunit number Rk,
while GCM (n,9)>1 for 3, 9, 21, 27, 33 and 39. These are all
composites except 3, especially 33 is a pseudoprime.
Accordingly we can say that if a number p is a prime and it is an originator of a repunit
Rk, then p must divide Rk. At a glance this condition is weaker than
the condition (p,9)=1. However most of pseudoprimes are to be rejected just by this rule.
Because it is a remarkable peculiarity that the length k of a
recursion unit of a prime is very long, but that of composites especially of
pseudoprimes are very short as you see in the table. Hence it usually comes to k <<
n, and then n cannot divide Rk.
Does there exist anything more? GCM (n,k) may be something. Let's check k=6 case. Here is
two primes 7 and 13, and two composites 21 and 39.
| n | recursion unit U | k | Rk\n | (n,9) | (n,k) | p/c | |
| # | 7 | :14285 7 | 6 | 15873...0 | 1 | 1 | p |
| # | 13 | :07692 3 | 6 | 8547...0 | 1 | 1 | p |
| # | 21 | :04761 9 | 6 | 5291...0 | 3 | 3 | c |
| # | 39 | :02564 1 | 6 | 2849...0 | 3 | 3 | c |
If n is prime, then n and k are mutually prime. We can detect 21 and 39 as composites by this rule. Maybe this condition is not so significant as we know that it is always k < n and if k not equals n, then it is of course that p is not mutually prime with k as p is supposed to be prime. Now let's summarize the necessary condition of a number p to be a prime,
| (1) p has a repunit R_k=pU(p)/9 (2) k divides p-1 (3) for p > 3, (p,9)=1 (4) p divides R_k (5) p and k are mutually prime |
(1) and (2) corresponds to Fermat's theorem. However
Fermat's theorem could not develop conditions (3) and (4). Especially rule (4) is strong
enough to separate pseudoprimes from prime numbers. But what about the sufficient
condition? I wonder if the above conditions are already sufficient for a number n to be a
prime.
Michiro
p.s. Allow me a correction: As you see in the above, the table in my
mail http://groups.yahoo.com/group/theory-edge/message/10962
was wrong at least at one point.
> 33= 0:30 >> 0:990, correctly:
#33=0:03 >> 0:99
This line reads the number 33 is of #type and the non-recurrent part of 1/33 is 0, recursion unit U(33)=03, and the
number has repunit 11. This number is a composite and the first Fermat pseudoprime.
-------- Original Message No.12 --------
Subject: Re: [theory-edge] Re: Recurrent Number
Date: Tue, 08 Mar 2005 06:15:37 +0900
From: babalabo <babalabo@aya.or.jp>
To: theory-edge@yahoogroups.com
Hi Dick!
Be pleased! I've got the proof for [8']. Recall the Fermat's Theorem.
| Fermat's Little Theorem |
| If p is a prime number and b a natural number, then (1) bp=b mod p. Furthermore, if p does not divide b, then there exists some smallest exponent d such that (2) bd-1=0 mod p, and d divides p-1. Hence (3) bp-1-1=0 mod p. |
| [8'] | Let p be a prime number which is neither 2 nor 5, and the recursion unit of p be U, then pU/9 is a repunit number Rn, i.e., pU=10n-1. |
Proof of proposition [8']: By the premise, p and 10 are mutually
prime, i.e., p does not divide 10. Hence by Fermat's theorem there exists a smallest
exponent n such that 10n-1=0 mod p. This means that p divides 10n-1.
Consequently there must be some smallest integer U such that pU=10n-1. We are
able to rewrite this equation in a form of integer division
A\B=Q...R, that means the quotient of A/B is Q and the remainder is R. Now we obtain in
this form, 10n\p=U...1. That is, we divide 10n by p and get the
quotient U and the remainder 1. This implies that U is the recursion unit of p. QED.
In factoring practice Fermat's theorem is used for a primality test. I don't know actually
what is like their Fermat primality test algorithm, but of course our theorem [8'] is also
applicable for the purpose and supposedly our method is much simpler and easier to
implement and perhaps faster. Because we need just to divide 1 directly by the number p.
It is a good idea to test every base b < p, and if every expression of pU in each
b-base forms a repunit number, then it is almost sure that p is a prime. Regretfully this
test is incomplete because it is known that there exist Carmichael numbers (the smallest is 561) that give zero
remainder for any choice of the base b a mutually prime to p. BTW a composite which
satisfies Fermat's theorem for some b is called a (Fermat)
pseudoprime.
The Fermat's theorem is applicable just for prime numbers. however as far as we observe,
theorem [8'] is extensible to general composite with #type, ie,
numbers which has neither factor 2 nor 5.
| [9] | Let m be an integer without factor 2 nor 5, and the recursion unit of m be U, then mU/9 is a repunit number Rn, i.e., mU=10n-1. |
I wonder if Fermat's Little Theorem is extensible in this manner. Because the proof of
theorem [8'] almost owes to Fermat's theorem. But as our test samples are so small,
proposition [9] may not be true. Anyway we've succeeded to establish theorem [8'] and as
far as I understand it might be quite possible that we discovered the fact for the first
time.
Michiro
p.s. The Fermat's theorem contains much more content than we used in the proof above.
Let's take a look at equation (3). Now we know that if p is a prime, then 10p-1-1
is also divisible by p. Consequently there exists some integer V satisfying pV=10p-1-1.
You may think that this equation is mostly the same with the above. But it is not. Unit U
has a condition "smallest", while V does not. surely V never be the recursion
unit of p. Needless to say a recursion unit U of any number x is only one. In other words
(3) expresses that there exists one more repunit which has factor p other than (2). This is the very prime that we were seeking in the sky.
| [10] | A prime number p is a factor of at least two repunit numbers such as R* =(10n-1)/9 and R+ =(10p-1-1)/9, where n is the smallest number that satisfies 10n-1=0 mod p, and n divides p-1. |
Proof of [10]: almost similar to the proof of [8']. QED.
In general the repunit number R* is relatively small but R+ may
become a huge number. This is the real picture that I described as "in
the sky". But now we understand that at least there does not exist an orphan prime
in the universe. To hear that I'm somewhat relieved. aren't you? The distance between
these two primes is surely astronomical, but I believe that we can use this knowledge in
any way because only if given number m, we can compute R* and R+
quite easily by just a simplest calculation. In this sense, the distance is not to fear at
all.
-------- Original Message No.11 --------
Date: Mon, 07 Mar 2005 22:58:05 +0900
To: theory-edge@yahoogroups.com
From: babalabo <babalabo@a...>
Subject: Re: [theory-edge] Re: Recurrent Number
Hi!
| I'd like to be able to help, but I am not a programmer, I don't know graph theory, your notational conventions and nomenclature are very confusing to me and while I am sure I could figure out where you are coming from, I find myself unmotivated to do so because I spend all of my ultra-precious spare time on my own researches. Your idea of |
That's OK. let's take it slow. No hasty travel. To test a narrow range is easy and enough for now. Maybe I can write it in a few days.
| using a single number as an encoding reference for factoring is an idea parts of my research are pointing to, but the number I have in mind for the job is not a repunit. If you can back up a bit, |
Very interesting!
| simplify, define the terms you are using, give some concrete, finite examples such that I may more easily understand what you are talking about, then I would be of help to the extent of my ability. At |
I'll write a brief note for the account later.
| present, unfortunately, your conundrums pale in comparison to my own, but I'm certain that is due only to my miscomprehension. I am |
Our directions are seemingly very close.
| presently preparing a paper for publication and it has taken my spare time over a 4 month period just to Tex up 11 pages. I am figuring the final paper will have 30-40 pages, but I may split it up into 2 or 3 papers (which will be more work in the long run actually). |
I've never experienced Tex but if it's like that, I may throw it out.
| I had looked into some stuff in the arena you are dwelling in very briefly. I take the rational number >1 formed by the ratio of 2 primes, discern the repeating string from the decimal expansion, and repeat the repeating string to the left (backwards) until I obtain the sequence of rational numbers all >1 which remain faithful to the repeating pattern even to the left of the decimal. |
OK.
| For the very few scant, low numbers I checked, when the original rational number is > 1 and is the ratio of 2 primes, it seems all digits to the right of the decimal are faithful to the repeating string, thus the differences between the original number and each number (>1) of the derived sequence is always an integer. The nature of these integers as dependent on the nature of the numerator and denominator of the original rational number was the particular focus of my interest at the time, but I didn't go very far with it. It is |
I'm afraid if the integer part is not so significant. For example, 199/29=6+25/29=6+25*1/29. Consequently at least in my eyes what you are dividing is not a prime but a composite 25=5*5.
| on one of my many dozens of back-burners for future investigation, though my current,
favored research also involves the decimal expansions of rational numbers in a different
way. I will try to upload a mathematica file to the file area that contains some simple examples of what I have described. Here are a few lines from that file I find particularly interesting because my process applied to the ratio of prime 199 over 29, yields first sequence integer 1 and 199/31 yields -1. When I get back to it, I had planned to try and write a routine to examine other twin primes to see under what circumstances they give 1/-1 like that, and also to find any instances where prime numerators and denominators forming rationals>1 failed to yield integers for the sequence (which I have not yet found). N[199/29,40]=6.862068965517241379310344827586206896552 6.862068965517241379310344827586206896551724137931034482759`40. -5.862068965517241379310344827586206896551724137931034482759`40. 1.00000000000000000000000000000000000000 N[199/31,40]=6.419354838709677419354838709677419354839 6.41935483870967741935483870967741935483870967741935483871`40. -7.41935483870967741935483870967741935483870967741935483871`40. -1.00000000000000000000000000000000000000 Other examples yield primes and composites alike and no patterns immediately emerge, but I only scratched the surface. Typically, when I research, my spinal column, which knows more truth than my brain proper, will send me signals that what I am looking at is worth |
My signals may come up from my stomach...
| pursuing. I recall getting those signals at the time I spent a little time on this one, I really do believe there is more to the story here, but I also believe that many, many, many mathematicians have been down this road before, so there must be something out there |
Agree.
| already. I have already wasted years discovering things that were already discovered, so I choose my battles carefully and try to do the best I can to make sure the war isn't already over before I take |
I'm always rambling around the ancient site of theaters listening to the voices of wind talking about their passion, ambition and regrets...
| up the fight. If there were any programming skills to be thrown toward this endeavor, I should like a tool with which to generate and examine the properties of my integer sequences and indeed, study which numbers always give rise to integer sequences and those that always give rise to non-integer rational sequences. But even better, would be references to related work that has already been completed. |
Today I was going to write a small test program for the conjecture [8'], but could not
[complete] as my computer (bombed yesterday) was very bad state and I cannot repair it
yet.
Michiro
-------- Original Message No.10 --------
Date: Mon, 07 Mar 2005 01:34:35 +0900
To: theory-edge@yahoogroups.com
From: babalabo <babalabo@a...>
Subject: Re: [theory-edge] Re: Recurrent Number
Hi Richard and all!
I showed a case method for factoring using Repunit
Table. I think that it works anyway, but not so good as the search space is
relatively too large comparing the fruit to be obtainable. I would like to propose a much
more effective method to search factors in a systematic way.
Assume we have an efficient algorithm B to determine if a value is prime or not. Then apply the test program B to the nodes in G and remove every nodes decided to be prime from the graph. If the graph G becomes null, then our job is complete. But it is almost sure that the graph G is not empty. Regretfully we can no longer factor those nodes by only our method because no two nodes ni, nj share individual prime p in the graph.
I don't know how much unfactored nodes would remain there, but could only say that
factoring must be an endless job for human. It might be that another prime of the same
value is contained in a larger repunit Rn untested. But these numbers are far
in the sky. so we are reluctant to call our method Separation of the Sky and the
Ground. The worse, there might be no partner even in the sky, i.e., the
occurrence of the prime might be just once on the ground, so to say an orphan in the universe.
However if this is the case, we may still have a clue to manage the situation as we know
that if a prime p appears in a repunit Rn just once, then the recursion unit U
of p must be a factor of Rn. I don't know how can we resolve this
formula/cryptograph for now but here is a hope.
To use different/multiple decimal bases simultaneously is a good idea because it is very
unlikely that two different systems have the same unfactored node set. I think that the sky and the ground method is very attractive because you can
start at just 100*100 GCM computations for a vast 100-digit whole space. Are you
satisfied?
Michiro
p.s. In our convention the greatest common divisor is abbreviated as "GCM" but it might be "GCD"
else where. Can anyone test the sky and the ground method? As I could only reserve the
time bound to this weekend for the subject. (Another excuse: I still haven't a multiple-precision arithmetic.)
But! I've happened to notice a big hall in my argument up to this point. Evidently question Q(4) is not answered/proven yet.
| Q(4) Does there exist a prime number p such that p does not divide any repunit number Rn? If yes, then show the minimum one. |
| A4: No. every prime number p except 2 and 5 appears in a Repunit Table. Let the recurrent unit of p be U and get the product pU. We already know that pU has a form of 999...9 since we assumed that p is a prime and neither 2 nor 5. Thus we obtain a repunit number R=pU/9=111...1 which has a factor p and p shall sit in the table. |
I think that it was not "we already know" but "we just know empirically". See http://groups.yahoo.com/group/theory-edge/message/10962 . In other words proposition [5] is not a theorem but an observation/conjecture.
| [5] | Every recurrent number n of type '#' is a divisor of some number m of length k such as 111...1=(10k-1)/9. As well a recurrent number of type '>' divides a number such as 9999...90. |
So at least we need to formally prove the following proposition.
| [8'] | Let p be a prime number which is neither 2 nor 5, and the recursion unit of p be U, then pU/9 is a repunit number Rn, i.e., pU=10n-1. |
However I have a confidence of [8'] to be true and even if it isn't, the sky and the
ground method is still valid. If [8'] does not hold, then there might be a prime which is
not in any repunit and said to be not so much an orphan as missing/drafting in the
universe at all. Anyway the following question is the most essential and crucial.
Q'(4) prove or disprove the proposition [8'].
This is a great chance/challenge for you. Bite it!
-------- Original Message No.9 --------
Subject: Re: [theory-edge] Re: Recurrent Number
Date: Sat, 5 Mar 2005 19:41:03 +0900
From: Baba Labo <babalabo@aya.or.jp>
To: <theory-edge@yahoogroups.com>
Hi Dick and all!
I wrote,
| If this dream comes true, then their effort turns from searching a star in the sky to building a public resource like Human Genome Project. of course I don't think that this is any easy but believe to be possible. You may wonder how are recurrent decimals relevant |
Now I found a solution, just a simple one. Assume that we have an efficient algorithm A
for computing GCM (Greatest Common Deviser). Then just check our Repunit
Table with the algorithm A and find a repunit number Ri which is not
mutually prime with the number n. Clearly A gives us a factor x of n. to perform this we
need both of
(1) An efficient GCM algorithm A, and
(2) A small enough lookup table R[n].
I believe that we possess the both. It is very good for us that we need not each entry of
repunit number of the table to be already factored. The factor x of Ri would be
given on the fly. I don't know if this method is actually applicable on the factoring
world. But it seems at least for me to be worthwhile to try. If the 10-base repunit table
is too sparse for practical purpose, you can adopt 2-base repunit table, i.e., Mersenne Table alternatively. If you are experienced in
factoring, please estimate the cost for factoring the smallest unfactored number n in your
table with this method. If you think it is not applicable at all, tell me your reason.
Michiro
p.s. It is possible that I accidentally send someone a mail with a file attached. If you
receive one, please don't open it and just throw it into your trash bin. As I wrote in my
previous mail I received a mail from an old member of this mailing list. A file was
attached to the mail and I opened it with the secret key in the mail. It was a warm
worm named Win32.Beagle. Fortunately my virus checker killed
it in the egg.
However I've received a delivery errmsg from cs.umass.edu. It says that my mail addressed
to a person in the host is infected by a virus named W32/Netsky.p@MM.
If this causes trouble on you, I apologize you deeply for my carelessness.^^;
-------- Original Message No.8 --------
Subject: Re: [theory-edge] Re: Recurrent Number
Date: Sat, 5 Mar 2005 19:28:51 +0900
From: Baba Labo <babalabo@aya.or.jp>
To: <theory-edge@yahoogroups.com>
I'm sorry. It was due to my setting of the internet access.
----- Original Message -----
From: "dgdegiorgi" <degiorgi@hispeed.ch>
To: <theory-edge@yahoogroups.com>
Sent: Saturday, March 05, 2005 5:01 PM
Subject: [theory-edge] Re: Recurrent Number
>
>
> Very strange.
>
> Clicking the Link I give, I get a page with a picture of the book
> and a lot of links to the chapters.
>
> The whole book is in
>
>
http://www.ams.org/online_bks/conm22/conm22-whole.pdf
>
> (1.4mb)
>
> Daniele
>
-------- Original Message No.7 --------
Subject: RE: [theory-edge] Re: Recurrent Number
Date: Sat, 5 Mar 2005 13:53:37 +0900
From: babalabo <babalabo@aya.or.jp>
To: <theory-edge@yahoogroups.com>
Hi Daniele!
Thank you very much for your ever unchangeable kindness.
| I have no substantial contribute to the discussion, but some factorizations of bn+1 and bn-1 can be found in a free e-book http://www.ams.org/online_bks/conm22/ |
It seems that they changed the link to the book. But this works. http://www.ams.org/online_bks/conm22/conm22-chVI.pdf
| There are the factorizations of 10n-1 for 1<=n<=150 and of odd n < 330. |
Yes, it was my expectation. But actually my downloaded copy has only 2 pages of VI. How
to Use the Main Tables, and the main tables themselves are missing. Perhaps they changed
their policy because that is a part of their commercial products. Anyway thanks a lot.
BTW this morning I've received a mail from our legend, Dan Pehoushek. Really surprised!
but my reply returned for some delivery failure. Dan, are you there? Please bite, no need
of hesitation!
Michiro
Rem: The missing link was my mistake. But "Dan" really bit
me with less hesitation.
-------- Original Message No.6 --------
Subject: RE: [theory-edge] Re: Recurrent Number
Date: Sat, 5 Mar 2005 02:12:15 +0900
From: babalabo <babalabo@aya.or.jp>
To: <theory-edge@yahoogroups.com>
Hi Richard!
| I'm glad you found the information you were seeking. |
Thanks a lot. I've earned a great crop.
| You say that as if unfactored 100 digit numbers shouldn't be so |
Yes, I was thinking so far.
| plentiful. 100 digits primes are easy to find and prove, but factoring a 100 digit number is still very intensive and time consuming. |
I've gradually got the situation. The Cunningham
Project is a big project for many years spending enormous amount of human
power. They are maintaining a large scale of tables to be filled and collaborating through
network. An astronomical effort like a planet search project.
I don't think that we have yet enough knowledge of recurrent decimals, I'd like to show
you how it could combine to their factoring table. Let's call the table of repunit numbers
Repunit Table. As you see this table is a very sparse table, so to say
exponentially sparse. If we can use this table as a lookup table for factoring, that will
be fine. But beforehand I would prove the question Q(4). just as easy.
Q(4) Does there exist a prime number p such that p does
not divide any repunit number Rn? If yes, then show the minimum one.
A(4) No. every prime number p except 2 and 5 appears in a Repunit Table.
Let the recurrent recursion unit of p be U and get the product pU. We
already know that pU has a form of 999...9 since we assumed that p is a prime and neither
2 nor 5. Thus we obtain a repunit number R=pU/9=111...1 which has a factor p and p shall
sit in the table.
How can we use this table for factoring? To make the story simple assume that we have a
function F(n) which gives an index value of the table, and each repunit number has its own
(not necessarily unique) key. Given composite number n, you can compute the value by F(n),
seek the table and find some Rn entries which match to the value. Every Rn
is already factored and you will get a bunch of primes to be tested. Once you've found a
factor, then you can go on until finish the factoring just repeating this procedure.
If this dream comes true, then their effort turns from searching a star in the sky to
building a public resource like Human Genome Project. Of
course I don't think that this is any easy but believe to be possible. You may wonder how
are recurrent decimals relevant to factoring. But perhaps you've heard somewhere that division is equivalent to multiplication. In fact I told my
schoolgirl like that, and it's the point where I began reflecting on it to myself.
Let's take a look at some sample. Let U(n) denote the recurrent recursion
unit of number n. then U(3)=3, U(7)=142857, and U(21)=047619, while 142857=47619*3, and we
earn U(7)=U(21)*U(3). Regretfully this doesn't work on the other side. But too early to
abandon. we are just at the beginning.
Michiro
Rem: Apparently this proof above is incomplete as "we already
know just empirically". However we would get a genuine proof later.
-------- Original Message No.5 --------
Subject: RE: [theory-edge] Re: Recurrent Number
Date: Fri, 4 Mar 2005 04:38:16 +0900
From: babalabo <babalabo@aya.or.jp>
To: <theory-edge@yahoogroups.com>
Hi!
The number M(k)=111...1 has a name, repunit number,
given by Beiler in 1966. http://mathworld.wolfram.com/Repunit.html, thanks Richard. From the
naming "repeating-unit", I guessed that he had been considering what we call recursion unit when he named it, but it may be just a unit
"1". The factoring table which I proposed in my first mail is maintained
on line by Brillhart et al since 1988, which I asked Vlad if the table is useful. BTW
repunit number Rn is a special case of Cunningham number bn-1,
and R2 corresponds to Mersenne numbers. Now we will use
repunit number Rn instead of our M(k) numbers.
Def: repunit number Rn=(10n-1)/(10-1)=(10n-1)/9.
Rem: In general repunit number Rn of b-base system is defined as Rn=(bn-1)/(b-1).
| [8] | A repunit number Rn can be prime only if n is prime. |
Proof of [8]: Assume n is a composite n=ab. Then 10ab-1 is a binomial number and can be factored algebraically. If a is even and a=2m then we get 102mb-1=(10mb-1)(10mb+1). Assume a odd, then
(10a-1)(10a(b-1)+10a(b-2)...+1)=(10-1)(10a-1+10a-2...+1)(10a(b-1)+10a(b-2)...+1).
Hence Rn cannot be a prime, contradiction. QED.
Another proof of [8]: Assume n is a composite n=ab, then it is easy to
see that Ra divides Rn as well as Rb. For example, R12=111111111111
is divisible by R2=11, R3=111, R4=1111 and R6=111111.
QED.
Q(3) Repunit number Rn is prime only if n=2
and R2=11.
A(3) No. there exist repunit prime numbers other than 11. We succeeded to
factor 18 digits Rn, and the next R19 was the second prime repunit.
Only seven repunit primes are known at present including R2=11, like n=2, 19,
23, 317, 1031, 49081, 86453. Madachy showed R2, R19, R23,
R317 in 1979, Brillhart and Williams proved R317 in 1977, Williams
and Dubner took R1031 in 1986. Granlund completed a search up to 45,000 in 1998
using two months of CPU time on a parallel computer. It was extended by Dubner in 1999
with the discovery of R49081, and by L. Baxter R86453 in 2000.
Q(4) Does there exist a
prime number p such that p does not divide any repunit number Rn? If yes, then
show the minimum one.
I think that my question Q(4) is still open. Considering that Williams and Seah [1979]
already factored the range of 2<=k<=1000 and told nothing of this, supposedly Q(4)
may not hold. However as you see the factoring repunit table R[n] is a
very sparse table, it is too early to say that it surely doesn't.
M.N.
p.s. Although I wrote that all of Rn up to n=1000 are factored, according to
some sites, there still remain so many unfactored numbers even in the 100 digits order.
check http://homepage2.nifty.com/m_kamada/math/11111.htm.
-------- Original Message No.4 --------
Subject: RE: [theory-edge] Re: Recurrent Number
Date: Thu, 3 Mar 2005 22:31:46 +0900
From: babalabo <babalabo@aya.or.jp>
To: <theory-edge@yahoogroups.com>
Hi Dick!
I've found my conjecture stating, "|K| is zero for every recurrent number" Q(2.2) was wrong. I checked the decimal numbers 1/n for n=2
to 50.
record format: [-#+>], [ n], [K:U], [K*n:U*n], [|U|=length of U],
[prime/composite]
recursion type: -:non-recurrent, #:recur, with no overlap :999...9,
>:recur with null overlap 0:999...90, +:recur with non-null overlap.
- type: 2,4,5,8,10,16,20,25,32,40,50 (11)
# type: 3,7,9,11,13,17,19,21,23,27,29,31,33,37,39,41,43,47,49 (19)
> type: 14,15,18,22,26,30,34,35,38,42,45,46 (12)
+ type: 6,12,24,28,36,44,48 (7)
'+'Type numbers are those I missed. As you wrote,
"the repeater is 000... iff n has form 2a5b". This is the
case '-' type. '#'Consists of prime numbers other than 2 nor 5, and their products. '>'
and '+' are mixed products of '-' and '#'. We know that every numbers are products of some
prime numbers. +Type number is a product of 2 and 5. #Type is without 2 and 5. > and +
types contain both (2 or 5) and others. Now we can say,
| [1] | A multiple m=n*x of a recurrent number n is recurrent too. |
| [2] | A multiple m=x*y of non-recurrent numbers x, y is non-recurrent. |
| [3] | Every non-recurrent number n is to be expressed as 2p5q, and any other numbers are recurrent. |
| [4] | Especially all prime numbers are recurrent, excluding 2 and 5. |
| [5] | Every recurrent number n of type '#' is a divisor of some number m of length k such as 111...1=(10k-1)/9. as well a recurrent number of type '>' divides a number such as 9999...90. |
| [6] | A number n of form 111...1 is of type '#'. |
| [7] | For any recurrent number n, the length k of recursion unit U of n is smaller than n. |
Proof of [6]: Apparently n is divisible by neither 2
nor 5. QED.
Proof of [7]: Compute one digit Q[i] of the quotient Q of 1/n step by
step. If remainder R=10i-SQ[i] (sorry, not accurate...) appears more than once,
then the quotient Q already contains a recursion unit. In other words, the remainder R
must be different for each computation until it begins recursion, while R < n implies i
< n. QED.
A(1) No. See the proof [7] above.
A(2) Yes. Type '+' is the case. (Type '>'
is assumed to be K=00..0.)
Q(3) Prove or disprove: suppose a number n of form
111...1 of length k, if k is prime then n=11.
Q(4) Does there exist a prime number p such that p does not divide any number n of form
111...1. If any, then show the minimum one.
Rem: I was somewhat confused. Question (2) consists of two parts, (2.1) and (2.2). I meant here that Q(2.1) was wrong. While Q(1) had asked if the proposed proposition table was totally true or not, but Q(2) was not in the table and I did not asserted in that way. So A(1) may not be determined yet...
-------- Original Message No.3 --------
Subject: RE: [theory-edge] Re: Recurrent Number
Date: Thu, 3 Mar 2005 14:52:16 +0900
From: babalabo <babalabo@aya.or.jp>
To: <theory-edge@yahoogroups.com>
Hi Max!
| After all, those numbers must be all rationals. Because they are repeated over and over in speeches, writings, books, etc. Don't you think? |
It may be if it is that sanity is doing the same thing over and over and expecting the same results. BTW I might have confused/mistaken radical and rational so far. As far as I recall it was said, "radical is rational" by Mao, the founder of the communist party of China.
-------- Original Message No.2
--------
Subject: RE: [theory-edge] Re: Recurrent Number
From: "babalabo" babalabo@aya.or.jp
Date: Thu, 3 Mar 2005 14:32:46 +0900
To: <theory-edge@yahoogroups.com>
Hi Dick!
| If the decimal expansion eventually repeats, the number is rational. This is equivalent to the definition of rational. If it never repeats, the number is irrational. |
Sorry. I've made my same old mistake once again. ^^;
| The non-zero, non-repeating parts "K" are much more the rule than the exception and all numbers that share a particular, eventual repeating pattern have common factors. For example, amongst 1/n, the repeater is 00000... iff n has form 2^a 5^b. Each repeating pattern has an infinity of "K"'s to add in front. Put anything you like in front of the repeating pattern and you have a rational number, just like counting. |
You are right. but when I say a (non-)recurrent number n, n is assumed to be an integer implicitly but not a general rational number. I claim that every non-recurrent number(integer) has a form of 2a5b, further I conjectured that |K| is zero for every recurrent number. This is equivalent to your "the repeater is 00000... iff n has form 2a5b." To consider a recurrent/non-recurrent number makes things very simple.
| As far as length of the repetition string, I recall seeing something on it on Mathworld awhile back, but the subject heading escapes me at the moment (maybe try rational number). There are proven bounds, if not exact formulas for the "rep length", I am pretty sure. |
As far as I've checked on some small samples, it seems that the length doesn't become so much long. Although currently as I have not a multi-precision arithmetic, my experiment is very restricted. What about the length of K, non-repeating part, for non-recurrent number n?
Michiro
-------- Original Message No.1
--------
Subject: [theory-edge] Recurrent Number
Date: Thu, 3 Mar 2005 06:49:24 +0900
From: babalabo <babalabo@aya.or.jp>
To: Theory-Edge <theory-edge@yahoogroups.com>
Hi Vlad and all!
I've dropped into a puzzle while I was helping a schoolgirl's homework. Say that a
decimal number n=0.xxxxyyyy... has two parts, non-recurrent part xxxx and recurrent part
yyyy.... We know that an irrational number has a non-recurrent part of infinite length,
while a radical rational number has a finite (possibly zero) length
non-recurrent part. We say a number n is recurrent iff 1/n has an
infinite recurrent part; otherwise n is non-recurrent. e.g. 3 is
recurrent, but 2 is not. We call a minimal non-recurrent part in a decimal number n the
recurrent unit of n. E.g. the recurrent unit of 0.6123123... is '123'. Propositions,
| [1] | A multiple m=n*x of a recurrent number n is recurrent too. |
| [2] | A multiple m=x*y of non-recurrent numbers x, y is non-recurrent. |
| [3] | Every non-recurrent number n is to be expressed as 2p5q, and any other numbers are recurrent. |
| [4] | Especially all prime numbers are recurrent, excluding 2 and 5. |
| [5] | Every recurrent number n is a divisor of some number m of length k such as 111...1=(10k-1)/9. for example 57=3*19 divides 111...1 (18digits) into 1949317738791423. |
| [6] | Hence it can be said that a number n=111111...1 is to be expressed as a product of prime numbers p1,p2,...pk excluding 2 and 5. |
Q(1) Are these correct? number theory may be your
field, so I ask you a bit.
Q(2.1) Are there any recurrent numbers n of which recurrent unit are very long, for
example longer than n?
Q(2.2) Are there any recurrent numbers n which have non-zero non-recurrent part? i.e.,
0.KUUU..., where U is the recurrent recursion unit and K is not totally
of '0' sequence.
Michiro
p.s.: Consider the inverse of a recurrent number n=7, 1/7=0.142857142857... Thus its
recurrent unit U=142857. now multiply U by n, and then we get
U*7=142857*7=999999=9*111111. Here is a table of 111...1s up to k=10.
11=11
111=3*37
1111=11*101
11111=41*271
111111=3*7*11*13*37
1111111=239*4649
11111111=11*73*101*137
111111111=3*3*37*333667
1111111111=11*41*271*9091
You would notice that if digit k of m=111...1 is prime, then m is a product of *two* prime
numbers. Because if k is not a prime, then we can partition m into like
'111','111','111',..., and '111' recurs by itself, while a prime length m has no such a
recursion. I guess that to find a recurrent unit isn't any hard. any usage of the table?
Where does the theory go if we do use other decimal systems than 10?
Q(3) Are there any integers k such that M(k)=(10^k-1)/9 is a prime other than M(2)=11.
![]()
Definitions, Propositions and Questions
| (1) | base | b | A real number x can be represented using any integer number b as a base (alternatively radix or scale). The choice of a base yields to a representation of numbers known as a number system. In base b, the digits 0, 1, ..., b-1 are used (where, by convention, for bases larger than 10, the symbols A, B, C, ...are generally used. | |||||||||||||||||||||||||||||||||||
| (2) | integer division | \ | Integer
division is a division
denoted \ in which the fractional
part (remainder)
is discarded. Integer division can be defined as |
|||||||||||||||||||||||||||||||||||
| (3) | recurrent number | n | A rational number n is said to be recurrent on b-base iff the b-base decimal representation of 1/n is of infinite length | |||||||||||||||||||||||||||||||||||
| (4) | recursion unit | U U(b,n) |
The number expressed with a portion of the minimum recurrent digits of a decimal representation of the inverse 1/n of a number n on b-base decimal system. Sometimes the number/length u of the digits may be referred as u-length and denoted as |U|=u. For example in 10-base, for n=3, 1/3=0.3333... u=1 and U=3, and for n=7, 1/7=0.1428571428..., u=6 and U=142857, for n=24, 1/24=0.041666..., u=1, U=6. See definition (15). | |||||||||||||||||||||||||||||||||||
| (5) | non-recurrent part | K | Fixed digits of a decimal representation D of b-base number system of the inverse 1/n of a rational number n. D is seen to be 0.KUUU... For convenience if |K|>0 we sometimes regard K+U as the non-recurrent part of the number. | |||||||||||||||||||||||||||||||||||
| (6) | recursion unit length | k | The number k of digits of the recursion unit U of a recurrent number n. If k is 0, then n is non-recurrent. For convenience we use k=|U| notation. | |||||||||||||||||||||||||||||||||||
| (7) | repunit number | Rk Rb(u) R(b,u) |
A repunit number Rk is a number consists of k>0 copies of digit 1. In base 10, Kr=(10k-1)/9. Generally repunit on b-base is a number of the form S[i=0 to u-1]bi = (bu-1) / (b-1). R(b,u) denotes a repunit number Ru on b-base. Alternatively RBI(u) is used too. | |||||||||||||||||||||||||||||||||||
| (8) | recursion type | # > + - |
|
|||||||||||||||||||||||||||||||||||
| (9) | GCM (GCD,GCF) | (a,b) gcd(a,b) | Greatest common measure (alternatively divisor, denominator, factor) for natural numbers, a and b. If (a,b)=1, then a and be are mutually (relatively) prime. Sometimes would be expressed as gcd(a,b). | |||||||||||||||||||||||||||||||||||
| (10) | pseudoprime | A composite which satisfies all the conditions of Fermat's little theorem. | ||||||||||||||||||||||||||||||||||||
| (11) | originator | A recurrent number n such as nU=Rk, where U is the recursion unit of n and k=|U|. An originator generates a repunit number Rk, while Rk possibly has multiple originators. | ||||||||||||||||||||||||||||||||||||
| (12) | totient function | f(n) | The totient function
f(n) |
|||||||||||||||||||||||||||||||||||
| (13) | radical, non-radical, ultra-radical, fundamental numbers | A number n on a b-base system is radical (with the radix b) iff some factor of n is a factor of either b or b-1; otherwise n is non-radical. As well an ultra-radical number is a number such that all of its factors are a factor of either b or b-1, while a fundamental number is a number such that all of its factors are a factor of the base b. For example in 10-base, n=7, 11, 13, 17, 19, 23,.., 49, 77,... are non-radical numbers, and n=2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16,... are ultra-radical numbers, while n=14, 21, 22, 26, 33, 34, 39... are radical but not ultra-radical numbers. No prime p is non-radical simultaneously on the bases both b and bp-1. | ||||||||||||||||||||||||||||||||||||
| (14) | u-length | k u |
The length u=n of a repunit number Rn=(bn-1)/(b-1)=S[i=0 to n-1]bi. The term "u-length" is also applied to the length of a recursion unit U(b,n) as (15), i.e., the period of recurring decimal on b-base of the reciprocal of a number n. | |||||||||||||||||||||||||||||||||||
| (15) | u-length function | y(b,n) | Given mutually prime numbers n and b, there exist nonnegative integer x<n and positive integers y and z such that z=x*by \n...x, that reads n divides x*by, the quotient z, and the remainder x, in other words, n*z+x=x*by. A set of {x,y,z} exists infinitely. u-length function y(b,n) is defined as the minimum such number y, as well recursion unit U(b,n) as the minimum such number z. Accordingly n*U(b,n) = r*(by(b,n)-1), where r is the first dividend that appears as the remainder. | |||||||||||||||||||||||||||||||||||
| (16) | multiplicative order, haupt-exponent, modulo order | e ordna On(a) |
Given numbers b and n, the smallest exponent e>=1 for which |
|||||||||||||||||||||||||||||||||||
| (17) | primitive root | g | If ordn g is actually equal to f(n) and therefore as large as possible, then g is called a primitive root modulo n. This means that the group U(n) is cyclic and the residue class of g generates it. Not every number n has a primitive root, but prime numbers always do. | |||||||||||||||||||||||||||||||||||
| (18) | generalized multiplicative order, discrete logarithm | m | If a is an arbitrary integer relatively prime to n, then there exists among the numbers 0,1,2,...f(n)-1 exactly one number such that a=gm mod n. The number m is then called the generalized multiplicative order (or discrete logarithm [Schneier,1996], or index [Nagell 1951]). |
< Propositions > C:Conjecture by MN, D:Proposal by DGD, T:Theorem
| [1] | C | A multiple m=n*x of a recurrent number n is recurrent too. |
| [2] | C | A multiple m=x*y of non-recurrent numbers x, y is non-recurrent. |
| [3] | C | Every non-recurrent number n is to be expressed as 2p5q, and any other numbers are recurrent. |
| [4] | C | Especially all prime numbers are recurrent, excluding 2 and 5. |
| [5] | C | Every recurrent number n is a divisor of some number m of length k such as 111...1=(10k-1)/9. For example, 57=3*19 divides 111...1 (18digits) into 1949317738791423. |
| [5'] | C | Every recurrent number n of type '#' is a divisor of some number m of length k such as 111...1=(10k-1)/9. As well a recurrent number of type '>' divides a number such as 9999...90. |
| [6] | T | A number n of form 111...1 is of type '#'. |
| [7] | T | For any recurrent number n, the length k of recursion unit U of n is smaller than n. |
| [8] | T | A repunit number Rn can be prime only if n is prime. |
| [8'] | T | Let p be a prime number which is neither 2 nor 5, and the recursion unit of p be U, then pU/9 is a repunit number Rn, i.e., pU=10n-1. |
| [9] | T | Let m be an integer without factor 2 nor 5, and the recursion unit of m be U, then mU/9 is a repunit number Rn, i.e., mU=10n-1. |
| [9'] | T | In b-base decimal system, for all non-radical numbers n, there exists a repunit number R(b,f(n)) originated from the number n, where f is the Euler totient function. This is equivalent to [14]. |
| [9"] | P2 T |
Schoolgirl's Homework Conjecture: Let y(b,n) be the minimum number of recurrent digits in b-base decimal expression of the inverse 1/n of a number n. Then for all natural numbers n>1 mutually prime to b and b-1, by(b,n)-1 is divisible by n, as well the repunit number R(b,y(b,n)) is a multiple of n. |
| [10] | T | A prime number p > 5 is a factor of at least two repunit numbers such as R*=(10n-1)/9, where n is the smallest number that satisfies 10n-1=0 mod p, and n divides p-1. Anothe one is R+ =(10p-1-1)/9. |
| [10'] | T | For any b-base system, a non-radical prime number p divides at least two repunits. One is R*=R(b,d)=(bd-1)/(b-1), where d divides p-1 and is the smallest number satisfying bd-1=0 mod p. And another one is R+=R(b,p-1)=(bp-1-1)/(b-1). |
| [11] | D1 T |
In every polynomial field, xk-1 is a multiple of x-1. Moreover if k is composite, say of the form p*q*r..., then xk-1 is a multiple af all xp-1, xq-1,xr-1,... |
| [12] | D2 T |
For each primes p,q,r,... > 5, there are infinite repunits multiple of p,q,r, ... and each combination of them (p*q, p*r, p*q*r, ...). |
| [13] | D3 T |
Daniele's Formula: For a prime number p, the repunit (10((p-1)*pk^k)-1)/9 is multiple of p(k+1). This implicitly implies [9]. |
| [14] | D4 T |
Given a number b and a number n relatively prime to b, then for all k bk*f(n)-1 is a multiple of n where f(k) is the Euler totient function. |
| [15] | T | For any b-base decimal system and natural numbers m and n, if n is divisible by m, then R(b,n) is divisible by R(b,m). Let q=n/m, then there exist two possible expressions of R(b,n) like R(b,n) = R(b,m)*R(bm,q) = R(bq,m)*R(b,q). Essentially equivalent to [11]. |
| [16] | T | For any b-base decimal system and natural numbers m and n, if n is a square of m, i.e., n=m2 then R(b,n) is divided by R(b,m), like R(b,n) = R(b,m) * R(bm,m). That is, a repunit R(b,m2) is a product of two repunits R(b,m) and R(bm,m) of the same u-length m. Corollary of [15]. |
| [17] | T | For a non-radical prime p on b-base, repunit number R(b,(p-1)*p) is divisible by p2. A repunit R(b,(p-1)*p) is factored by two repunits of u-length p and p-1 respectively in two ways like R(b,(p-1)*p) = R(b,p-1) * R(bp-1,p) = R(b,p) * R(bp,p-1). Each of these repunits are multiple of p. This result is extendable to [13]. |
| [18] | P1 T |
For any natural number n>2 on b-base decimal system, the value of u-length function y(b,n)>0 always divides the value of Euler's totient function f(n), i.e., gcd(f(n),y(b,n)) = y(b,n). If n is a prime, then y(b,n) divides n-1. |
| [19] | C | For any b-base decimal system, for any number n with y(b,n)>0, the quotient f(n)/y(b,n) is an ultra-radical number on the base b, where f(n) is the Euler's totient function and y(b,n) is the u-length function of n. |
| [20] | T | Multiplicative orders exist for n that are not factors of b, i.e., there exists the smallest exponent e>=1 such that be=1 mod n. This implies [9"]. By Fermat's little theorem, if n is prime, then e=n-1 satisfies the congruence, and by Euler's totient theorem e=f(n) also satisfies the congruence generally. Our claim [9"] is that e=y(b,n) not only satisfies the congruence, but also it is the smallest, i.e., the multiplicative order of b mod n. |
| [21] | P3 C |
A repunit R(b,k) is factored into distinct repunits and primes. |
| [22] | P4 T |
A repunit number R(b,k) originates itself on any b-base. |
| [23] | P5 C |
If the u-length y(b,n)=n-1 for a number n, then n is prime. Equivalent to [26]. |
| [24] | P6 C |
|
| [25] | P7 C |
(1) If n is fundamental, then y(b,n)=0.
(2) If n has just one non-radical prime factor, then y(b,n) is prime. (3) If n has more than one prime factors, then y(b,n) is composite. |
| [26] | C | Prime Criterion: A natural number n is prime iff there exists some base b such that y(b,n) = n-1. Equivalent to P4 [23]. Fermat's theorem implies the only if part of the statement. |
| [27] | C | Composite Criterion: If n is an odd composite, then there exists some base b such that factors of the psi number y(b,n) forms a factor of n like the following manner. Suppose y and n have factors like y(b,n)=f1*f2*...*, and n=p1*p2*...*. Then there exists some combination of factors taken from {f1, f2, ...} such that pi = fi1*fi2*...fik + 1. |
| Fermat's Little Theorem |
| If p is a prime number and b a natural number, then (1) bp=b mod p. Furthermore, if p does not divide b, then there exists some smallest exponent d such that (2) bd-1=0 mod p, and d divides p-1. Hence (3) bp-1-1=0 mod p. |
| Euler's Totient Theorem |
| A generalization of Fermat's little theorem. Let f(n) denote the totient function. Then bf(n)=1 mod n for all b mutually prime to n. |
| Lagrange's Group Theorem |
| If G is a finite group and H is a subgroup of G, then the order (that is, the number of elements) of H divides the order of G. This implies Fermat's little theorem, Euler's Totient theorem, and [18]. |
| (1) | Are these propositions correct? | ? |
| (2.1) | Are there any recurrent numbers n of which recurrent unit are very long, for example longer than n? | no |
| (2.2) | Are there any recurrent numbers n which have non-zero non-recurrent part? i.e., 0.KUUU..., where U is the recursion unit and K is not totally of '0' sequence. | yes |
| (3) | Prove or disprove: Suppose a number n of form 111...1 of length k, if k is prime then n=11. | false |
| (3') | Repunit number Rn is prime only if n=2 and Rn=11. Right? | no |
| (4) | Does there exist a prime number p such that p does not divide any number n of form 111...1. If any, then show the minimum one. | no |
| (4') | Does there exist a prime number p such that p does not divide any repunit number Rn? If yes, then show the minimum one. | no |
| (4") | Prove or disprove the proposition [8]. | true |
| (5) | If for all prime p there are repunits multiple of all powers of p, or not. (DGD) | ? |
| (6) |
| Lehmer's Totient Problem |
| If there exist any composite numbers n such that f(n)|n-1, where f(n) is Euler's totient function. If such a number exists, then it must be a Carmichael number because y(b,n)|f(n)|n-1, and then bn-1=1 mod n. No such number is known so far. |
![]()