１−３．ｋ端子分割困難なグラフがある

■メッシュ図検定は，無試行判定によって非ハミルトングラフを検出することのできる初めての方法となったが，この方法を開発する直接のきっかけとなったのはｋ端子分割困難なグラフがあるという事実だった．つまりｋ端子分割で左右部分グラフの確定パスを突き合わせるためのコストは端子点の個数をｋとするとｋ！になるから，大きなｋに対してほとんどそれはＮ！に近いものとなってしまう．ｋ端子分割は再帰的に実行されるから，あるグラフのｋ端子分割を行うときはつねにそのグラフの極小なｋ端子分割を対象とすればよいことになるので，ｋ端子分割困難なグラフとは，グラフの極小なｋ端子分割を与えるｋの値がある定数値，たとえば20を越える10ようなグラフである．

■メッシュグラフはまさにこのようなグラフの実例であった．たとえばｍ×ｍメッシュグラフの場合，点数はＮ＝ｍ^2となるからグラフを縦断ないし横断する端子分割ではｋ＝となり，ｋ端子分割困難である．（方形メッシュグラフの場合，メッシュ図の４隅にはより小さいｋ端子が存在しているからリンゴをかじるように小さいｋによる端子分割を進めることも可能だが，メッシュグラフの中にはまったくｋ端子分割困難なグラフが存在する．）ｋ端子分割検定はきわめて高速に収束する強力な手法であったから，その方略で歯が立たないグラフに対しては，別の戦術を考えるしか方法が無かった．

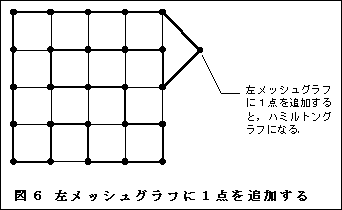■グラフのトポログラフィーから見ると，極小なｋ端子分割を与えるｋの値はそのグラフの短径と考えてもよいだろう．つまりｋ端子分割困難なグラフとはウエスト周りの大きい寸胴肥満型のグラフである．正準な右メッシュグラフ（欠けた枝のない偶数点メッシュグラフ）は完全ハミルトングラフ11である．左メッシュグラフも非ハミルトングラフではあるが，１点を任意に追加ないし削除して偶数点メッシュグラフに変更することで，ハミルトングラフに変えることができる．ｋ端子分割検定から考えると途方もなく困難なグラフであったメッシュグラフも，メッシュ図の上に乗せてみると意外に扱いやすいグラフであることが分かった．

■直並列検定，メッシュ図検定，ｋ端子分割検定の３種類の検定を併用する検定の方法を３種検定と呼ぶ．３種の検定はそれぞれの判定規則によって非ハミルトングラフを分離することができる．あるごく一部のグラフは３種の検定のすべてで非ハミルトングラフであると判定される．あるグラフは２つの検定法から，非ハミルトングラフであるとの判定を受ける．しかし，いずれの検定法によっても分離することのできない非ハミルトングラフも存在する．直並列検定とメッシュ図検定は無試行判定法を持っているから，即時に判定を下すことができる．ｋ端子分割検定は分割されたグラフを再帰的に検定するという方法だから即時判定を行うことは，原理的に不可能である．ダイアモンド図形は即時判定可能であり，これはｋ端子分割検定で無試行判定が可能となるような例外である．

10 ｋ＝２０のときｋ！は，１０＾18 のオーダーの値になる．これは現在の最高速のコンピュータを使って計算してもおそらく１０日以上かかるだろう．

11 任意の枝を通るハミルトン閉路の存在するグラフ