2-2. IO-division Experiment

There exist two kinds of IO-division experiment, as (1)k-terminal division experiment, (2)cut-set division experiment. Both of them can prevent 2-factor rule offenses against Hamiltonian postulate by dividing a graph into two parts of right subgraph and left subgraph and examining their interface between two subgraphs. Moreover, it may brings drastic reduction of experimentation costs to execute the experiments recursively with capped subgraph closing the conjunction part of the divided subgraphs by branches of a clique.

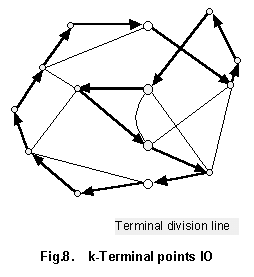
Def.2-2.1 k-terminal division

Let such minimal points set that a connected graph is separated into two subgraphs by removing a points set of the graph be a terminal points set. Then k-terminal division is a graph division with conjunction part of the terminal points set comprising k points.

Any branch of the graph belongs to either two subgraphs on k-terminal division. And also branches connecting terminal points are delivered arbitrarily to either subgraphs.

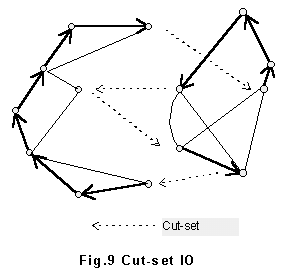
Def.2-2.1 cut-set division

Similarly, cut-set division is a graph division with conjunction part of cut-set, where let such minimal branches set that the graph is separated into two connected components by removing a branches set be a cut-set.

Supposing that a Hamiltonian tie is a cyclic waterway, since a water current in-flowing from right subgraph must surely flow out from left subgraph, same number of in-flows and out-flows must exist at the conjunction part of the graph division. Owing to this, on k-terminal division experiment we can make the experiment as below.

(1) If there exist odd terminal points, at least one of them must be a blockade point. Hereon, we say that a blockade point is a terminal point where exists no water current through the conjunction part. Therefore, branches (of the Hamiltonian tie) incident with blockade points only belong to either right or left subgraph.

(2) At the conjunction part, number of passage points must be even. Moreover, directions of water current passing through the conjunction part must be the same number in right and left hand. We say a passage point is a terminal point having an in-flowing branch in either right or left subgraph and an out-flowing branch in opposite side.

(3) As these constraint condition become tight by determining or removing branches incident with terminal points, it comes able to determine or remove corresponding branches automatically conforming to those constraint.

In the same way, in cut-set experiment we make the experiment conforming to following constraints.

(1) If there exist odd cut-set branches, at least one of them must be a blockade branch (contradictory branch or obstacle branch).

(2) Number of cut-set branches intersecting with a Hamiltonian tie must be even. Furthermore, these branches must contain same number of in-flowing branches and out-flowing branches viewing from one side of subgraphs. We call in-flowing branches and out-flowing branches generically passage branches.

(3) As these constraint conditions become tight by determining or removing cut-set branches, it comes able to determine or remove corresponding branches automatically conforming to those constraints.

The condition that number of passage points or passage branches must be even is stronger rule than the rules of auto-determination or removal in factor experiment procedure and it can detect latent contradictions, which are in the stage that cannot be detected by factor experiment before it happens under the judgment with non-retrial as IO contradictions. In k-terminal division experiment, non-2-connected graphs can be detected by judgment with non-retrial. And also, cut-set experiment detects a part of non-2-connected graphs by judgment with non-retrial.

Although either of division experiments is able to put forward sub-experiments dividing a graph into two parts, k-terminal graph division might be more favorable concerning the number of elements of the conjunction part.